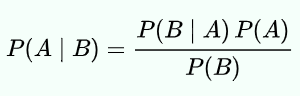君子は豹変すべし(ベイズ更新)
Back to Top「君子は豹変す」という諺があります。
”豹変”という言葉を聞くと「考えをコロコロ変えて主義主張が無い」ような悪いイメージがあるかも知れませんが、諺の本来の意味は「(出来る人は)過ちを速やかに改め、自らを一新する」であり良い意味で使われるものです。
昔のドキュメンタリー番組で優秀なプロジェクトマネージャが「決断しないで後悔するよりも、決断して後悔する方を選ぶ」とおっしゃっていました。
今回は逐次情報を得ながら自身の持つ”信念”を更新していく「ベイズ更新」についてお話しようと思います。
ベイズの定理の復習
#以前のブログ記事で「ベイズの定理」についてご説明しました。
ベイズの定理は以下の式で表されます。
ここでAとBは事象であり、式として成立するためにP(B)は0ではないです。
P(A|B)は「Bを前提としてAが発生する確率(事後確率)」を示します。(条件付き確率)
P(B|A)は上記の逆で「Aを前提としてBが発生する確率」を示します。
P(A)やP(B)は、条件なしにAやBがぞれぞれ観測される確率(事前確率)を示します。
AとBは独立した事象であることが前提です。
ベイズ更新とは
#ベイズ更新とは、一つ前の事象で確認された事後確率を、次の事象の事前確率として使用し事後確率を”更新”していく手法を言います。
いま事象Bが複数あると考えましょう。
事象をそれぞれ B1、B2、B3 とします。
事象B1のときにAが発生するベイズの定理を
P(A|B1) = P(B1|A)*P(A)/P(B1) ・・・式1
と置きます。
事象B2、B3も同様に
P(A|B2) = P(B2|A)*P(A)/P(B2) ・・・式2
P(A|B3) = P(B3|A)*P(A)/P(B3) ・・・式3
と置きます。
ベイズの定理の式は、最初に考えていた主観確率(事前確率:P(A))がデータを得ることで新しい主観確率(事後確率:P(A|B))へ更新される式と見ることができます。
式1では、事前確率P(A)が事象B1の条件を受けて事後確率P(A|B1)に更新されます。
次に新しいデータB2がインプットされたとします。
すでに元々考えていた事前確率P(A)はP(A|B1)に更新されているので、式2のP(A)にはP(A|B1)の値が入っています。
そして式2の右辺のP(A|B2)も式3のP(A)に代入され、次々に事後確率を更新していくのです。
事前確率から事後確率への更新のことを「信念の更新」と表現されることもあります。
データを得て次々に確率が更新されていく様は、人間が何かのデータを得て”古い考え”を”新しい考え”に改めていく処理に似ています。
まさに「君子は豹変す」です。
例題を通して「君子は豹変す」を体感してみましょう。
例題「パスアラウンドレビューの結果を受けて」
#あるソフトウェア開発組織ではコロナ禍の影響により、レビュー会をリモートで行うことが増えていた。
今回実施するレビュー会(仕様書レビュー)は仕様書をメールに添付してレビューアに送付し、後日指摘を返信してもらう「パスアラウンド」形式で実行することにした。
パスアラウンド形式のレビューは簡易に実施できる反面、複数のレビューアからの指摘が衝突した場合の調整等に手間がかかるなどの弊害があったが、レビューアのレビュー会スケジュール調整が困難であったためパスアラウンド方式を採用した。
今回のパスアラウンドレビューにはB1,B2、B3の3人にレビューアとなってもらった。
これまでの調査から各レビューアについて以下のことが分かっているとする。
次工程で問題が発生した製品の仕様書レビューで”不合格”判定を出した確率
次工程で問題が発生しなかった製品の仕様書レビューで”不合格”判定を出した確率
B1氏の場合は以下の確率表だった。
| レビュー不合格 | レビュー合格 | |
|---|---|---|
| 問題発生 | 95% | 5% |
| 問題未発生 | 20% | 80% |
B2氏の場合は以下の確率表だった。
| レビュー不合格 | レビュー合格 | |
|---|---|---|
| 問題発生 | 80% | 20% |
| 問題未発生 | 40% | 60% |
B3氏の場合は以下の確率表だった。
| レビュー不合格 | レビュー合格 | |
|---|---|---|
| 問題発生 | 85% | 15% |
| 問題未発生 | 30% | 70% |
B1,B2,B3の3人のレビューアの事前評価は以下に要約できる。
B1氏:問題検出力”高め”
B2氏:問題検出力”低め”
B3氏:問題検出力”そこそこ”
レビュー依頼者は、今回の仕様書の品質を「良い」と考えている(主観確率)。
事前確率を「次工程で問題が発生する確率は10%」と置いた。
信念の更新
#レビュー開始前の事前確率は
次工程で問題が発生する確率は10%
です。
レビューが進行するに従ってこの”信念”がどのように変化するでしょうか。
レビュー依頼者が仕様書を各レビューア(B1,B2,B3)に送付しました。
ある程度の時間が経って、B1氏からレビュー結果が戻ってきました。
結果は「不合格」でした。
式1
P(A|B1) = P(B1|A)*P(A)/P(B1) ・・・式1
を計算しました。
結果は
P(A|B1) = 0.95 * 0.1 / ( 0.95 * 0.1 + 0.2 * 0.9 ) = 0.35
であり、事後確率は35%となりました。
最初に設定した「次工程で問題が発生する確率は10%」からかなり増加しましたが、レビュー依頼者は「まだ慌てる時間じゃない」と感じています。
次にB2氏からレビュー結果が戻ってきました。
結果は「不合格」でした。
式2
P(A|B2) = P(B2|A)*P(A)/P(B2) ・・・式2
を計算しました。(ただし、上式のP(A)は更新された事前確率(35%))
結果は
P(A|B2) = 0.8 * 0.35 / ( 0.8 * 0.35 + 0.4 * 0.65 ) = 0.51
となり、事後確率は51%となりました。
先に更新した”信念(35%)”よりも更に悪化しています。
レビュー依頼者も流石に「あれ?ちょっとまずいかも」と考えています。
更にB3氏からレビュー結果が戻ってきました。
結果は”今度は”「合格」でした。
式3
P(A|B3) = P(B3|A)*P(A)/P(B3) ・・・式3
を計算しました。(ただし、上式のP(A)は更新された事前確率(51%))
結果は
P(A|B3) = 0.15 * 0.51 / ( 0.15 * 0.51 + 0.7 * 0.49 ) = 0.18
となり、事後確率は18%となりました。
先に更新した”信念(51%)”より大幅に改善されています。
このように情報を追加する毎に
事前確率:10% →(情報B1)→ 事後確率:35% →(情報B2)→ 事後確率:51% →(情報B3)→ 事後確率:18%
と確率が更新されました。
最初に設定した「次工程で問題が発生する確率は10%」からは悪化しているものの、3名のレビューアの情報を元にして、今回の仕様書の品質をある程度”定量的に”説明できる状態になったと言えます。
逐次合理性
#逐次合理性・・・。
なんだか難しそうな言葉ですが、要は「最終結果は事象の発生順序による影響を受けない」ことと考えれば良いです。
上記の例題で言えば、レビュー依頼者は事後確率をレビューアからの返信順のB1→B2→B3で更新しましたが、レビューアからの返信がB3→B2→B1の順となっても最終結果は変りません。
B3→B2→B1の順番で計算したときの事後確率の変化は
2% → 5% → 18%
と変化します。
最終結果は変っていません。
パスアラウンドレビューにおいて、返信の早さ遅さが結果に影響していないことがわかります。
まとめ
#ベイズ更新は「人間が情報を得て、考えを変えていく過程」に似ています。
ベイズ更新を「プロジェクトの失敗確率」の指標として使うことも可能だと思います。
プロジェクトは上流から要求分析、仕様、設計、実装、試験、評価の順に進んでいきます。
品質を確認する”関所”を設け、メトリクス等のデータを得ながら事後確率(プロジェクトの失敗確率)を計算するなどの応用が考えられます。
実はプロジェクトマネージャーは知らず知らずのうちに頭の中で「ベイズ更新」を実施していて「マズイかな」とか「大丈夫かな」という”信念の更新”を実施しているのだと思います。
「君子は豹変す」
まあ、世の中には頭の固い人も多いのですけどね。
データ分析に活用して頂ければ幸いです。