ロボットマニピュレータ制御のアルゴリズム

(株)豆蔵　エンジニアリングソリューション事業部　石井隆寛

1. はじめに

（株）豆蔵では様々なロボット技術を開発している。他社製ロボットを用いてクライアントの要望に応える応用技術を開発することが多いが、自社でも6軸や7軸のアームを持つ産業用ロボット、いわゆるロボットアーム＝マニピュレータを一から開発している。この開発を通じて様々な応用技術や提案を生み出している。今回ここで得た知見を読者の方と共有したいと思う。本解説では6軸の産業用垂直多関節型マニピュレータを例にしてこれを制御するさまざまなしくみを説明したい。特に基礎となるアルゴリズムや関連の数学を紹介する。ROS（Robot Operating System）の技術的背景も理解できるので、ロボットの応用や改良に役立つことを期待する。今回は最も基本的な軌跡生成処理を解説する。

2. ロボットマニピュレータとは

本体構造

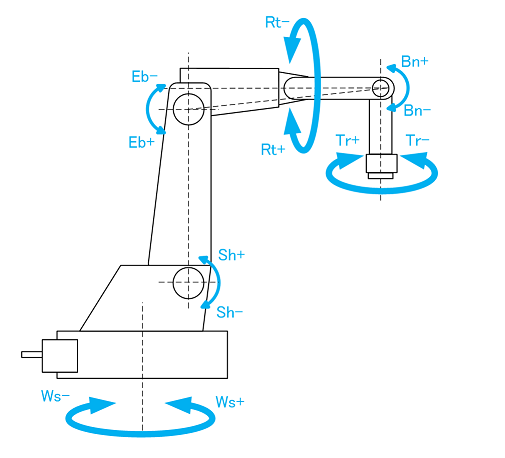
まずは制御対象となるハードウェアがどんなものなのか説明したい。下図は典型的な産業用マニピュレータである。人間の腕を模したもので、6個の回転関節軸の先に5個のリンク（骨）を有しており様々な手先の動きを再現できる。各軸は下から順に

Ws軸（Waist：腰）
Sh軸（Shoulder：肩）
Eb軸（Elbow：肘）
Rt軸（Wrist Rotation：手首旋回）
Bn軸（Wrist Bending：手首曲げ）
Tr軸（Wrist Turning：手首回転）

と呼ばれる。（ほかに[S軸, L軸, U軸, R軸, B軸, T軸]や単純に[J1軸,J2軸,J3軸,...,J6軸]と呼ばれることもある。）

Tr軸の先にはツール（ハンド）を装着する。例えば溶接機、レーザ装置、グラインダー、ドライバー、ドリル、吸引機、グリッパー、カメラなど作業用途に応じて取り替える。

各軸には、ACサーボモータと減速機と機械式ブレーキがあり、これらを回転動作させることにより正確なハンドの位置と姿勢を3次元的に制御する。通電有無により積極的に機械式ブレーキを解除したり逆に利かせたりできる。突発的事態で給電や通信が途絶した場合、自動的に機械式ブレーキがかかり、危険な自重によるアームのフリーフォールを防ぐことができる。

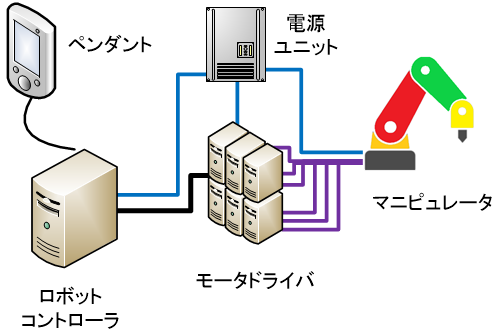
主要周辺機器

＜モータドライバ＞

指定した角度、指定した角速度、または指定したトルクになるようモータへの通電電流を制御するコンピュータである。サーボモータ内の回転角度センサを利用したフィードバック制御と各種信号フィルタにより、迅速かつ滑らかなモータ動作ができるよう工夫されている。通常、モータ1個に対して1個のモータドライバが接続されており、本体制御には計6個のモータドライバが必要である。

各モータとは回転角度センサ用の通信ケーブルと給電ケーブルでつながれる。モータへの給電と自身の演算のための電力は電源ユニットから得る。

＜ロボットコントローラ＞

統括的に6個のモータドライバへ指令を出すメインコンピュータである。EtherCAT、LAN、シリアルI/O等、各種通信I/O装置であるとともに、本稿で述べる制御のための各種数値計算を実行する演算装置でもある。6個のモータドライバとEtherCATやCANなどの通信規格で結ばれ、複数モータ間の同期をとったり、各モータドライバに指令値を送信したり、実際に到達できた値を受信する。
また、ペンダントなどのヒューマンユーザインタフェーズ（HUI）からの指令を受け、ロボットプログラムの解釈、実行、環境設定、データ記録を行う。さらに、ロボットにツール制御のための機器が加わった場合それらとのI/O、およびロボット動作に同期した制御も行う。

＜ペンダント＞

HUIとなるコントローラである。各軸毎に正転/逆転を指示したり、手先を3次元で直線/円状に移動したり姿勢を変えるためのJOG操作ボタンを備える。また、ロボットに複雑な動作指示をするためのプログラムを表示、編集、実行する機能を備える。

＜電源ユニット＞

AC電源から各種機器に電力を分配する。変圧してサーボモータのAC電源や周辺機器のDC電源となる。大電流を扱うのでリレーなど機械的なスイッチが装備されることが多い。

本体動作のしくみ

以上のような構成のもと、下記の処理を繰り返すことでアームを動かすことができる。

ロボットコントローラで、動作に必要な6軸分の関節角度 $\Theta$ を求める。
$\Theta$ 要素の各角度値を対応するモータドライバに送り実行指令する。
$\Theta$ の各指令角度値に達するまでサーボモータが回転し各関節が動く。
ロボットコントローラで、各モータドライバが実際に到達した角度 $\Theta_{act}$ を得る。

ここで $\Theta$ はリンク間の関節軸角度 $\theta$ 、6個分を表すベクトルであり

\Theta = (\theta_{1},\theta_{2},\theta_{3},\theta_{4},\theta_{5},\theta_{6} )

である。
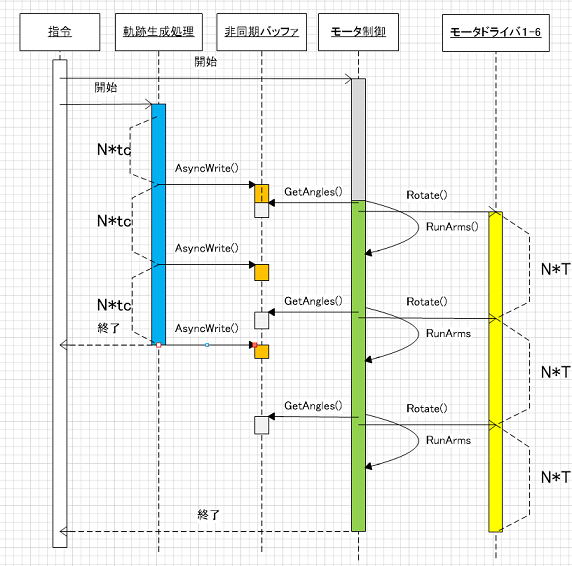
上記繰り返しを行える周期Tは、（機械性能やモータドライバの処理性能によって変わるが）1～2ミリ秒(ms)程度の固定値である。実際にはバッファリング、つまりあらかじめ $\Theta$ のサンプルを複数作成しておき、非同期I/Oとして一気にモータドライバに送る。例えば、T=1[ms]としてN=100単位時間分の時系列 $\Theta(t)(t=1\sim100)$ を一気に送信した後、実際にアームが稼働する時間はかっきり100[ms]=0.1秒(s)となる。この0.1(s)の間に次の100個分の $\Theta(t)$ をすべて計算して送信処理までできていれば、切れ目なくアームの連続稼働が可能となる。下記の図はこれを実現する処理シーケンスの例である。

次章ではこのしくみを利用してソフトウェアでマニピュレータをどう制御するのか説明する。

3. 基本制御アルゴリズム

マニピュレータの構造定義

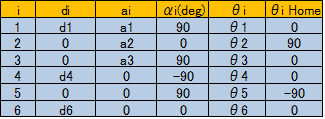
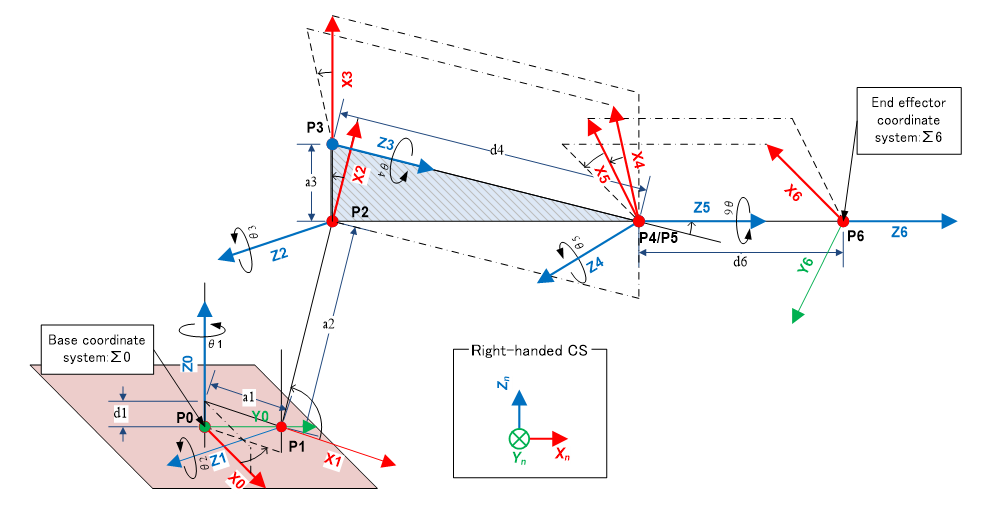
一般にマニピュレータのリンクやツールの位置関係を表す幾何構造をDHパラメータという形で表現する。関節回転軸にXYZの直交座標系を重ね、相対的に次の関節がどういう状態になっているか2つの距離と2つの角度で表す。下記がピューマ型マニピュレータのDHパラメータ表である。

これを図示すると下図のようになる。本解説で出てくる座標系はすべて右手系である。

DHパラメータは、ベースのXYZ座標系 $Σ_0$ から始めて先端に向かい

Z軸方向に $d_{i}$ 移動
Z軸周りに $θ_{i}$ 回転
X軸方向に $a_{i}$ 移動
X軸周りに $α_{i}$ 回転

を繰り返すことにより各回転軸に張り付いた $Σ_i$ を定義できる。 $P_i$ は $Σ_{i}$ の原点である。 $Σ_{6}$ がツールの座標系である。さらに延長してi=7を追加すればツール先端（手先） $P_{7}$ の座標系 $Σ_{7}$ を表すことができる。この中で $d_i$ , $a_i$ , $\alpha_i$ はロボット設計値で定数である。一方 $θ_i$ は関節軸角度であるため、サーボモータで制御する変数となる。

順運動学計算(Forward Kinematics)

$\Theta$ を与えられたときベース座標からみたツール先端の位置や姿勢はどうなるのか？ $P_7$ や $\Sigma_7$ の算出方法を考えてみよう。

まず、 $\Sigma_{i-1}$ から $\Sigma_{i}$ のアフィン変換を、4x4の行列としてDHパラメータで表すと下記のようになる。

A_i(\Theta)=\left( \begin{array}{cccc} \cos (\theta_i) & -\cos(\alpha_i)\sin(\theta_i) & \sin(\alpha_i) \sin (\theta_i) & a_i \cos (\theta_i) \\ \sin (\theta_i) & \cos(\alpha_i)\cos(\theta_i) & -\sin(\alpha_i)\cos (\theta_i) & a_i \sin (\theta_i) \\ 0 & \sin(\alpha_i) & \cos(\alpha_i) & d_i \\ 0 & 0 & 0 & 1 \\ \end{array} \right)

例えば $\Sigma_{1}$ の場合

A_1(\Theta)=A_1=\left( \begin{array}{cccc} \cos (\theta_1) & 0 & \sin (\theta_1) & a_1 \cos (\theta_1) \\ \sin (\theta_1) & 0 & -\cos (\theta_1) & a_1 \sin (\theta_1) \\ 0 & 1 & 0 & d_1 \\ 0 & 0 & 0 & 1 \\ \end{array} \right)

となる。 $\Sigma_{0}$ から見た $\Sigma_{i}$ のXYZ座標軸の方向と原点位置は

T_i(\Theta)=A_1 A_2 A_3 A_4 ... A_i

で計算できる。従ってツール先端の座標系 $\Sigma_7$ のときは

T_7(\Theta)=A_1 A_2 A_3 A_4 A_5 A_6 A_7

を計算すれば良い。ここで

T_i(\Theta)=\left( \begin{array}{cccc} u_x & v_x & w_x & q_x \\ u_y & v_y & w_y & q_y \\ u_z & v_z & w_z & q_z \\ 0 & 0 & 0 & 1 \\ \end{array} \right)

とすると、左上の3x3の部分行列 $R_i$ （正規直交系）がベース座標系 $\Sigma_0$ から見た、座標系の姿勢/方向を表し、4列目が原点の位置を表す。つまりi番目のXYZ座標系の3軸の方向は

\vec{X_i} = ( u_x,u_y,u_z )

\vec{Y_i} = ( v_x,v_y,v_z )

\vec{Z_i} = ( w_x,w_y,w_z )

であり、位置は

\vec{P_i} = ( q_x,q_y,q_z )

と表すことができる。

ここで3軸の方向はツール先端においては「姿勢」ということになるが、9個もの数値で表現するのは煩わしいので、ZYXオイラー角 $(\alpha,\beta,\gamma)$ 3個で表現する。Z軸周りに $\gamma$ 回転してY軸周りに $\beta$ 回転してX軸周りに $\alpha$ 回転したとすると、

R_i=R_z(\gamma) R_y(\beta) R_x(\alpha)

ここで $R_x$ はX軸周りの、 $R_y$ はY軸周りの、 $R_z$ はZ軸周りの3x3の回転行列を表す。これを解いて

\alpha=atan2(v_z, w_z);

\beta=atan2(-u_z,\sqrt{v_z^2 + w_z^2});

\gamma=atan2(u_y,u_x)

と計算できる。（※atan2(y,x)はArcTan(y/x)を計算するC言語の関数。）

以上、 $\Theta$ からツール先端の位置と姿勢を算出する計算を順運動学という。

逆運動学計算(Inverse Kinematics)

ロボットマニピュレータで最も重要な機能の一つは、ツール先端を指定した場所に、指定した姿勢で動かすということがある。そのため、順運動学の計算とは逆に、ツール先端の位置 $\vec{P}$ と姿勢 $R$ からその位置や姿勢が成り立つ軸角度 $\Theta$ を逆算しモータドライバへの指令値とする必要がある。この計算を逆運動学計算(IK)という。

指定した $\vec{P}$ と $R$ からツール先端の座標系を4x4の同次行列 $M_7$ で表し

M_7=T_7(\Theta)

と置く。一旦簡単のため両辺右から定数行列の $A_7^{-1}$ を乗じて

M_6=T_6(\Theta)

とおく。原理的にはこれらの要素で有効な12個の連立方程式を6個の $\theta$ について解けばよい。しかしながらこれは非独立かつ非線形の連立方程式となるため、最急降下法など手間のかかるアルゴリズムを利用する必要がある。特に収束計算が必要な解法の場合、収束までの繰り返し数が予測できないため計算時間が不安定となる。そのためIKがボトルネックとなってシステム稼働に支障をきたすことがある。これとは異なり、軸数や特別なマニピュレータの型によっては解析的解法が知られている。いずれにしてもこの連立方程式は一意には解けず、最大8通りの解の組み合わせがあることが知られている。

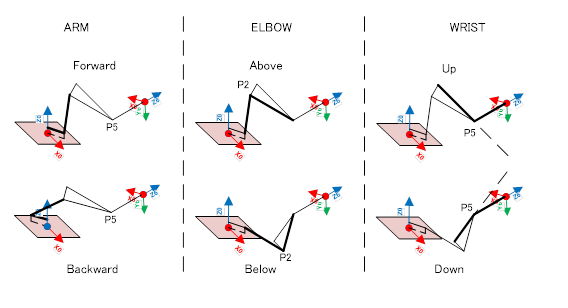
幸い本例のピューマ型の6軸マニピュレータでは解析手法がある。これは、公知の方法として幾何学を駆使して成り立っている手法である。しかし、幾何形態で言うと3種類の2択(ARM Forward/Backward, ELBOW Abov/Below, WRIST Up/Down （下図参照）)となり、組み合わせとしては最大 $2^3=8$ 通りの解の可能性を持つ。

そのため、形態を指定する、現在の $\Theta$ の値と最も近くなる組み合わせを選ぶ、など、何かしら合理的な選択手法が必要である。我々が実際に実装したIKのコア部分のコード（※1）を参考として下記に示す。

※1. 例外処理や検査処理の詳細は除いているのでこのままでは実用不可であることに注意。

///////////////////////////////////////////////////////////
/// @brief Find joint axis angle with inverse kinematics (IK) (holding mode setting)
///////////////////////////////////////////////////////////
int Kinematics::CalcJointAngles6ByIKwithMode(
						const Matrix4x4& T6,
						const JAngles6& prev_theta,
						JAngles6& theta,
						int mode[3],
						double& diff_average,
						bool bCheckRange) const
{
	JAngles6& th=theta; // angle
	JAngles6 dth; // difference between angle and prev_angle
	int ndif=0;
	diff_average=1.0e+10;
	const double &ux = T6.At(0,0), &vx = T6.At(0,1), &wx = T6.At(0,2), &qx = T6.At(0,3);
	const double &uy = T6.At(1,0), &vy = T6.At(1,1), &wy = T6.At(1,2), &qy = T6.At(1,3);
	const double &uz = T6.At(2,0), &vz = T6.At(2,1), &wz = T6.At(2,2), &qz = T6.At(2,3);

	const double &d1 = m_d1, &d4=m_d4, &d6=m_d6;
	const double &a1 = m_a1, &a2=m_a2, &a3=m_a3;
	const int mode_arm   = mode[0]; //Forward+/Backward-
	const int mode_elbow = mode[1]; //Above+/Below-
	const int mode_wrist = mode[2]; //Up+/Down- 

	//---------------------------------------------------
	// th[1]
	//---------------------------------------------------
	//P Position = O4 / O5 @ WC
	double px = qx-d6*wx;
	double py = qy-d6*wy;
	double pz = qz-d6*wz;
	int iret=0;
	double karm;

	//check Arm mode
	if(mode_arm>0){	//Arm Forward
		karm = 1.0;
	}else{			//Arm Backward
		karm = -1.0;
	}
	th[1] = atan2(karm*py, karm*px);
	iret=EvaluateAxisTheta(1, prev_theta, th, dth,  bCheckRange);
	if(iret<0) return iret;
	ndif++;

	//---------------------------------------------------
	// th[3]
	//---------------------------------------------------
	double C1=cos(th[1]);
	double S1=sin(th[1]);

	// k1*S3 + k2*C3 =k3 Solve
	double k1 = 2.0*a2*d4;
	double k2 = 2.0*a2*a3;
	double k3 = px*px +py*py +pz*pz	+a1*a1 -a2*a2 -a3*a3
					+d1*d1 -d4*d4 -2.0*( a1*(px*C1+py*S1) + d1*pz );
	double denom1 =k2+k3;
	double t=0.0;

	// Normal solution
	// (k2+k3)*t^2 -2*k1*t +(k3-k2) =0 Solve
	double D  = k1*k1 + k2*k2 - k3*k3;
	double rootD = sqrt(D);

	///   Elbow Mode: Above(+1)/Below(-1)
	if(mode_elbow>0){	//Above(+1)
		t = (k1-rootD)/denom1;
	}else{				//Below(-1)
		t = (k1+rootD)/denom1;
	}
	th[3] = 2.0*atan(t);
	iret = EvaluateAxisTheta(3, prev_theta, th, dth,  bCheckRange);
	if(iret<0) return iret;
	ndif++;

	//---------------------------------------------------
	// th[2]
	//---------------------------------------------------
	double C3=cos(th[3]);
	double S3=sin(th[3]);
	//----------------------
	// myu1*C2 + nyu1*S2=gamma1
	// myu2*C2 + nyu2*S2=gamma2 Solve
	double myu1 = 	a3*C3 +d4*S3 +a2;
	double nyu1 =	d4*C3 -a3*S3;
	double gamma1 =	px*C1 +py*S1 -a1;
	double myu2 = -nyu1;
	double nyu2 =  myu1;
	double gamma2 = -d1+pz;
	double denom2 = -myu1*myu1-nyu1*nyu1;
	double C2 =  (gamma2*nyu1-gamma1*nyu2)/denom2;
	double S2 = -(gamma2*myu1-gamma1*myu2)/denom2;

	th[2] = atan2(S2,C2);
	iret=EvaluateAxisTheta(2, prev_theta, th, dth,  bCheckRange);
	if(iret<0) return iret;
	ndif++;

	//---------------------------------------------------
	// th[5]
	//---------------------------------------------------
	const double th23 = th[2]+th[3];
	const double C23 = cos(th23);
	const double S23 = sin(th23);
	double C5 = -wz*C23+(wx*C1+wy*S1)*S23;
	const double th5 = acos(C5);
	double S5  = sqrt(1.0-C5*C5);

	/// Wrist Mode: Up(+1)/Down(-1)
	if(mode_wrist>0){
		th[5] = th5;  //Wrist Up
	}else{
		th[5] = -th5; //Wrist Down
		S5  = -S5;
	}
	iret=EvaluateAxisTheta(5, prev_theta, th, dth,  bCheckRange);
	if(iret<0) return iret;
	ndif++;

	//---------------------------------------------------
	// th[4],th[6]
	//---------------------------------------------------
	const double C4 = (wx*C1*C23+wy*C23*S1+wz*S23)/S5;
	const double S4 = (-wy*C1+wx*S1)/S5;
	th[4] = atan2(S4,C4);
	iret=EvaluateAxisTheta(4, prev_theta, th, dth,  bCheckRange);
	if(iret<0) return iret;
	ndif++;

	const double C6 =  ( uz*C23-(ux*C1+uy*S1)*S23)/S5;
	const double S6 =  (-vz*C23+(vx*C1+vy*S1)*S23)/S5;
	th[6] = atan2(S6,C6);
	iret=EvaluateAxisTheta(6, prev_theta, th, dth,  bCheckRange);
	if(iret<0) return iret;
	ndif++;

	//--------------------------------
	// Average angle calculation
	double d_sum=0.0;
	double d;
	for(int i=1;i<=6;i++){
		d = dth[i]/(m_theta_upper[i] - m_theta_lower[i]);// Normalize in the operating range.
		d_sum += d*d;
	}
	diff_average = d_sum;

	return 0;
}

速度の順運動学/逆運動学計算

$\vec{P_t}$ をツール先端の位置とすると下記の6x6の行列が計算できる。これは速度変換のヤコビ行列という。
ここで" $\times$ "はベクトル積、右肩のＴは行列の転置を表す。

J=\left( \begin{array}{ccccc} [\vec{Z_0} \times (\vec{P_t}-\vec{P_0})]^T & [\vec{Z_1} \times (\vec{P_t}-\vec{P_1})]^T & [\vec{Z_2} \times (\vec{P_t}-\vec{P_2})]^T & ... &[\vec{Z_5} \times (\vec{P_t}-\vec{P_5})]^T\\ \vec{Z_0}^T & \vec{Z_1}^T & \vec{Z_2}^T & ... & \vec{Z_5}^T\\ \end{array} \right)

このヤコビ行列を用いて下記のように関節軸速度からツール先端の並進速度および回転速度が計算できる。

\Omega=( \omega_1, \omega_2 , \omega_3 , \omega_4 , \omega_5 , \omega_6 )

\left( \begin{array}{c} {\vec{v_t}^T} \\ {\vec{w_t}^T} \\ \end{array} \right) =J \Omega^T

ここで $\omega_i$ {i=1,2,...,6}は各軸の角速度、 $\vec{v_t}$ はツール先端の3次元並進速度ベクトル、 $\vec{w_t}$ は3次元回転速度ベクトルである。
一般的には $J$ の逆行列 $J^{-1}$ は一意に求まるので、

\Omega^T = J^{-1} \left( \begin{array}{c} {\vec{v_t}^T} \\ {\vec{w_t}^T} \\ \end{array} \right)

とすれば逆にツール先端並進速度と角速度から6軸の角速度を求めることもできる。

これらの変換式はロボットの状態を表示したり、動作解析、力学計算等の特殊制御で活用される機会が多い。

軌跡生成

PTP制御とCP制御

以上のような基礎数学やアルゴリズムを用いて、

PTP(Point to Point)制御＝現在の状態 $\Theta_{s}$ から指定した $\Theta_{e}$ まで滑らかに動作できる $\Theta(t_j)$ を算出して関節を動かす制御。
CP(Continuous Path)制御＝ツール先端が一定の3D形状（直線、円弧など）に沿って滑らかに指定点や指定姿勢に到達できるような時系列 $T_7(t_j)$ を算出後、これらをIKにより $\Theta(t_j)$ を算出し関節を動かす制御。

を行う。（ここで $t_j$ はモータドライバに与えるサンプル周期T=1[ms]の等間隔時間列を示す。）

このような時系列サンプルを生成することを軌跡生成という。PTPの場合は $\Theta(t_j)$ の時系列を生成することを言い、CPの場合は $T_7(t_j)$ の時系列を生成することを言う。ここで注意すべきことはこの時系列は周期Tの等時間間隔の時系列でないといけないということである。いずれの場合も、開始地点と終了地点とその間での動作速度が必要である。

実際のUIでの軌跡の指定、例えばロボットプログラムでは下記のような指定の仕方をする。開始地点は現状のロボット姿勢の状態であり、各命令では終了地点のみ指定する。

20: JOINT 90,0,0,0,0,0 maxvr=30.0 
21: LINE_MOVE -400, 200, 200　maxvc=150
22: CIRCLE_MOVE  500, 300, 200　maxvc=150

これらの地点をKP(Key Point)と呼ぶ。JOINT命令のようなPTP命令では、開始/終了の2つのKP間で各軸がストレートに回転することを前提に、各軸の角速度が最大値maxvrになるよう6軸分の角速度プロファイルを決定し、 $\Theta(t)$ のサンプルを算出する。一方LINE_MOVEやCIRCLE_MOVEのようなCP命令ではKP間をつなぐツール先端の軌跡形状(それぞれ直線、円弧)とツール先端速度が最大速度maxvcになるような速度プロファイルを決定して、サンプル点 $T_7(t)$ を一旦算出する。最終的にはIK計算で $\Theta(t)$ のサンプルを算出する。

なお、速度プロファイルの設定には最高速度を指定することもあるが、開始KPから終了KPまでの移動時間を指定することもある。

速度プロファイルの決定方法

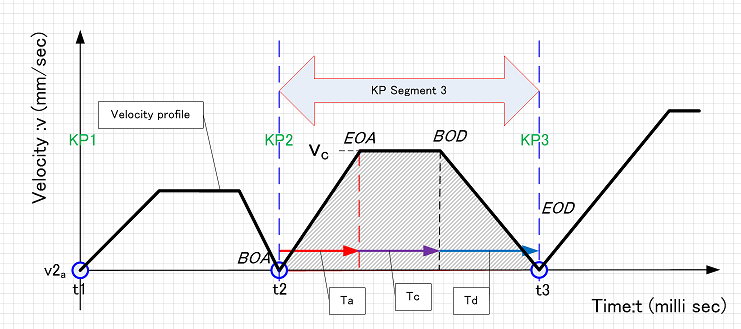
下記はCP制御時の速度プロファイルの一例で、台形速度プロファイルを示す。KP間の移動距離Sは軌跡形状から算出する。また $T_a$ , $T_d$ はシステム設定値としてあらかじめ決めて置き、最高速度 $v_c$ はユーザが指定する。速度の時間積分（＝面積）が移動距離になるので、Sが台形面積と等しくなるよう調整すれば台形の形状が決定できる。

この図のプロファイルはきっちり台形であり、BOAやEODまたEOAやBOD付近では加速度（プロファイルの一時微分）が突然変化する。そのため実際にこれで関節を動かすと、しばしば同付近で機械的衝撃や振動が生じてしまう。振動なく滑らかに動作させるために、この付近を高次関数や三角関数を利用した滑らかな曲線でつないで平滑化することが多い。このときは面積が台形面積Sと同じになるよう工夫する。

軌跡サンプリング

CP制御で指定された軌跡の形状は幾何学を用いて解析的に求めることができる。つまり適当なパラメータ $s_k$ でサンプリングした $T_7(s_k)$ {k=0,1,2...}の列として具体的に計算できる。ここで $T_7$ はツール先端の位置と姿勢を示す4x4の同次行列である。
しかし $T_7(s_k)$ 列は求めるべき等時間サンプリングの時系列 $T_7(t_j)$ 列とは明らかにずれている。どうやってこのずれを修正して、正しい時系列をサンプリングしたらよいだろうか？

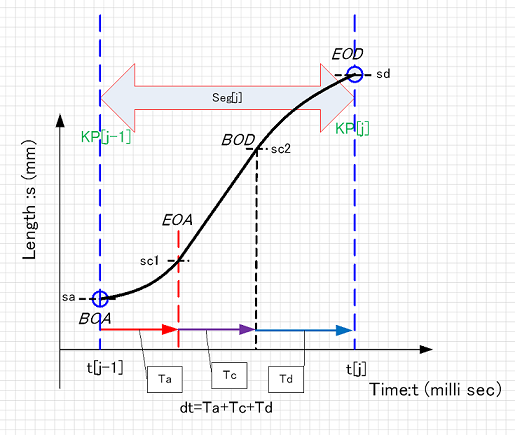
そもそもこのずれは、パラメータ $s_k$ と $t_j$ のずれから生じる。下記は速度プロファイルを積分したグラフであり、縦軸は移動距離 $S(t)$ になる。時刻が進むにつれ単調増加する曲線である。

一方 $T_7(s_k)$ から移動距離サンプル $S'(s_k)$ を幾何学的に計算できるが、これも $s_k$ に関して単調増加関数である。この場合は時刻とは無関係な関数である。軌跡形状が複雑な場合は曲線となることもあるがあくまで単調増加関数である。結局 $S$ も $S'$ もパラメータに対してone to oneの関係である。従って移動距離 $S$ を介してパラメータ $s$ と $t$ を対応づけることができる。すなわち、下記の処理が可能である。

$S(t_{j})$ の値を計算する。
$s_{k}$ ⇒ $S'(s_{k})$ 表を逆転し $S'(s_{k})$ ⇒ $s_k$ 表とみなす。この表から値 $S(t_j)$ で補間した値 $s_{intp}$ を求める。（線形補間で十分）
$T_7(s_{intp})$ を計算。これを $T_7(t_{j})$ と置く。

以上を $j=0,1,2,..$ として終了KPへの到達時刻まで繰り返せば、時系列 $T_7(t_j)$ のサンプル列が生成でき、ここに軌跡生成が完了する。なおPTP制御の場合はSの代わりに代表的な $\theta_i$ （※2）を用いて同様の処理を行うことができる。またCP制御のときは、求めた $T_7(t_j)$ をIKで変換すればモータ制御に必要な関節角度列 $\Theta(t_j)$ が得られる。

※2. 例えば、6個の $\theta$ のうち最大の動作をするものを代表とする。

4. 終わりに

マニピュレータの構造から始めて、その制御に必要とされる基礎的な考え方や数学を紹介した後、実際に動作させるための軌跡生成の方法について解説した。しかし以上の説明では下記のようなCP制御に関しては詳しく述べなかった。

軌跡の幾何学的サンプリングの具体的な方法は？例えばよく利用される、直線軌道、円軌道やスプライン軌道などは $s_k$ を用いてどう計算するのか？
ツール先端の姿勢変化（回転）はどうサンプリングするのか？
動作が異常になる「特異点」と呼ばれるアームの特別な姿勢、または $\theta_i$ の組み合わせがある。これは制御上問題となる。それは何であり、これをどう回避したらいいのか？

これらについては次回説明したい。

参考文献

遠山茂樹 (著)、　「ロボット工学 (メカトロニクス教科書シリーズ)」、コロナ社 (1994)
R.P.ポール (著), 吉川恒夫 (訳)、「ロボット・マニピュレータ―」、コロナ社（1984）

以上