2要因の分散分析
Back to Top前回のブログ記事では「1要因分散分析」を見てきました。
今回は2つの要因の分散分析について見ていきましょう。
要因が増えると何がおこる?
#コロナ禍になって出社勤務から在宅勤務に切り替えた会社さんも多いのではないでしょうか。
これまでは出社して皆で直接顔を突き合わせて実施してきた共同作業からリモート環境での共同作業に変わったときに、従来の作業パフォーマンスが出せているのか非常に気になるところだと思います。
出社形態を1要因と考えて、「出社」と「在宅」という条件の2水準を持つとしてみましょう。
単に出社形態の1要因だけで分析するなら、前回紹介した「1要因分散分析」で対応できます。
しかし、他の要因が関係してくるとそうはいきません。
要因単独で結果に与える影響を「主効果」といいます。
主効果についてはこれまでも1要因の分析を見てきたので大体のイメージはつかめると思います。
2つ以上の要因が関係している場合には、要因同士が影響しあう「交互作用」というものが発生します。
交互作用を言い換えれば「相乗効果」「相殺効果」と言えます。互いに何らかの影響を及ぼして、時には正の効果、また時には負の効果を及ぼします。
交互作用がある場合には個別の要因だけでは説明しえない影響が結果に現れます。
この交互作用を含めて分析する分析手法が分散分析です。
お題「出社と在宅でレビュー手法による結果に影響はあるか?」
#例えば、先ほどの出社形態の要因以外に、レビュー手法を要因にあげてみましょう。
レビュー手法には「ウォークスルー」「チームレビュー」「インスペクション」の3水準があるとします。
今回は以下の2要因
レビュー手段(3水準) × 出社形態(2水準)
について分散分析を実施してみましょう。
交互作用図
#いきなり分散分析を実施する前に、先ほど説明した「交互作用」を視覚的に説明したいと思います。
それにはまず交互作用図を見てみましょう。
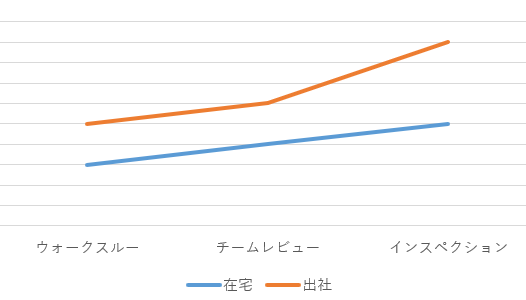
下図は今回のお題を概念的に表したものです。
あくまで概念的な話ですが、一番右側のデータは効果が大きくなる方向に働いているように見えます。(値の大小はあまり意味が無いとお考え下さい)
上図では作用を強めあっています。
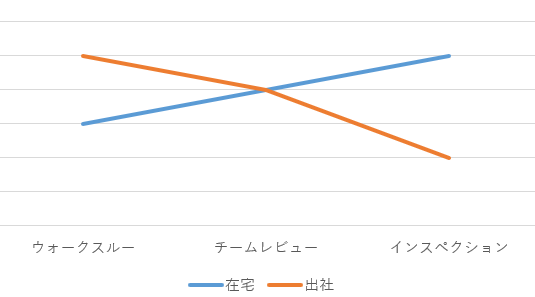
では次の図の場合はどうでしょうか?
効果が逆転してしまっています。
このように作用を弱めあう場合もあります。
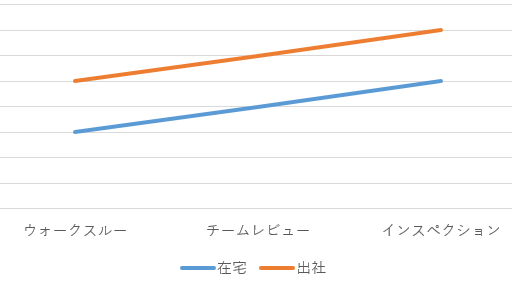
もし「出社」「在宅」でレビュー手法の間に「交互作用」が存在しない場合はグラフの線は下図のように平行になります。
サンプルデータ
#では実際に数値を当てはめて「交互作用」の有無やその度合を数値をもって示してみましょう。
以下のサンプルデータを考えました。
レビュー対象は仕様書として、数値は欠陥除去率で、単位は「件/頁」とします。
| 在宅 | 在宅 | 在宅 | 出社 | 出社 | 出社 |
|---|---|---|---|---|---|
| ウォークスルー | チームレビュー | インスペクション | ウォークスルー | チームレビュー | インスペクション |
| 3.5 | 3.7 | 3.8 | 3.7 | 3.9 | 4.1 |
| 3.4 | 3.8 | 3.8 | 3.7 | 3.8 | 4.1 |
| 3.3 | 3.9 | 3.9 | 3.8 | 4 | 4 |
| 3.6 | 3.5 | 4 | 3.6 | 3.8 | 4.3 |
| 3.7 | 3.6 | 3.9 | 3.5 | 3.9 | 4.3 |
| 3.5 | - | 3.8 | 3.7 | 3.8 | 4.1 |
| - | - | - | 3.8 | 3.8 | 4 |
| - | - | - | - | - | 3.9 |
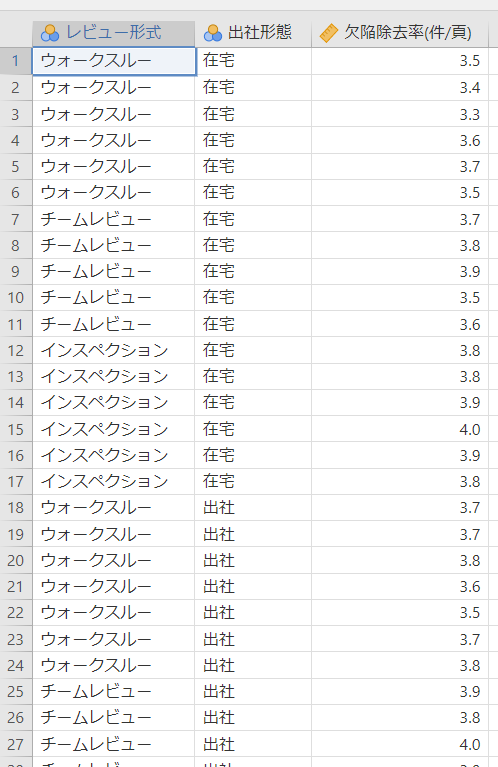
さっそくjamoviにデータを設定します。
要因と水準は
- レビュー形式(ウォークスルー、チームレビュー、インスペクション)
- 出社形態(在宅、出社)
を定義しました。
データパネル
※注意:データ行が長いので表の下側は見切れています。
記述統計での確認
#メニューの「分析」-「探索」-「記述統計」を選択します。
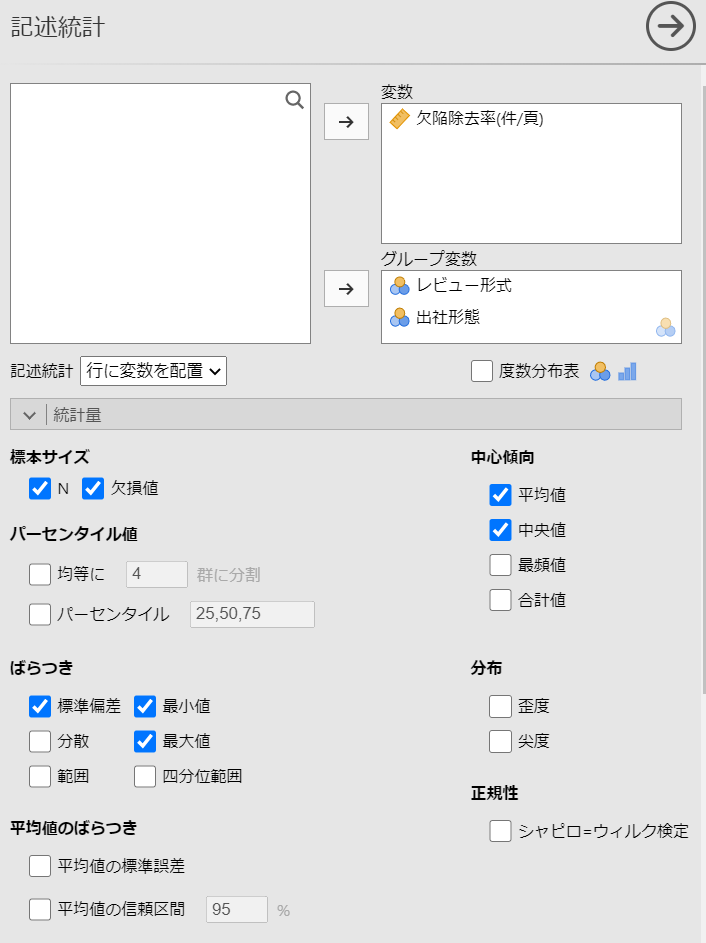
統計量の設定を以下のように行います。
(記述統計「行に変数を配置」を選択しています)
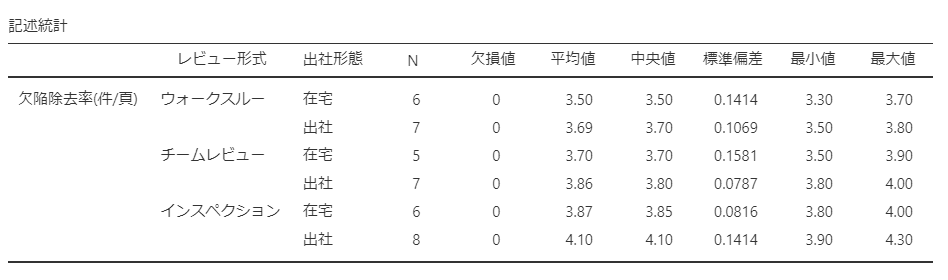
記述統計の結果が以下のように表示されました。
グラフでも確認してみましょう。
グラフは「棒グラフ」を選択します。
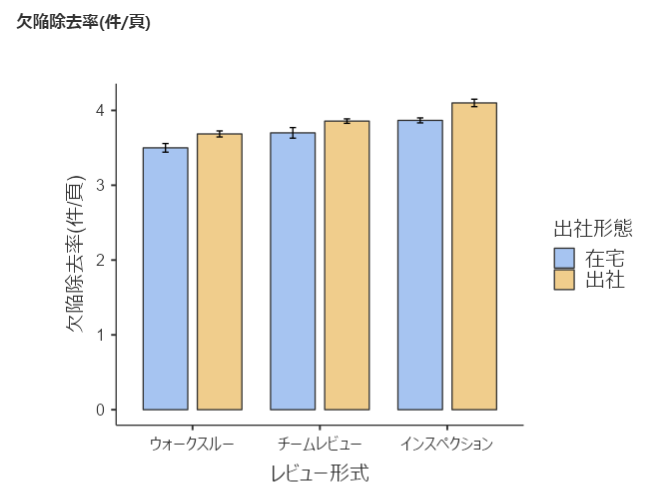
以下の棒グラフが表示されました。
総じて全体の傾向として、欠陥除去率は
インスペクション > チームレビュー > ウォークスルー
のように見え、また
出社 > 在宅
も確認できます。
これらを分散分析で確認していきます。
分散分析
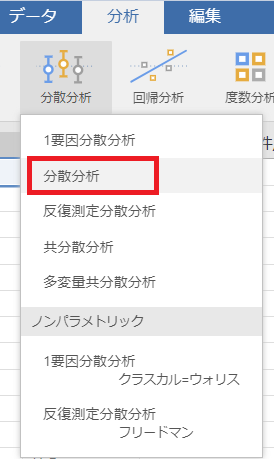
#メニューの「分析」-「分散分析」-「分散分析」を選択し、以下のように設定します。
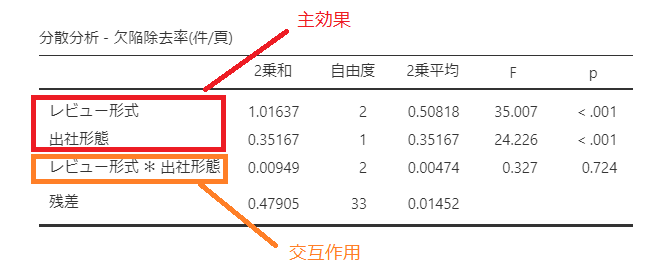
分散分析の結果が以下のように表示されました。
またいつものようにp値に注目します。
レビュー形式の主効果、出社形態の主効果はともに「<0.01」なので高度に有意となりました。
さて、レビュー形式と出社形態の間の交互作用「レビュー形式*出社形態」のp値は0.724となり「差が無いを”棄却”できない」となり、2つの条件の組み合わせでは有意でない(影響がない)ということが言えます。
つまり「レビュー形式」と「出社形態」に相乗効果、相殺効果は無いだろうということが言えます。
多重比較
#今回、レビュー形式と出社形態の主効果に有意差が見られました。
出社形態は水準が2つなので、影響を及ぼしあっている水準はおのずと決まります(2つしかないので、それぞれが効果を及ぼす)
しかし、レビュー形式には水準が3つ(ウォークスルー、チームレビュー、インスペクション)ありますので、どれとどれが効果を及ぼすのかを確認したいと思います。
そのような時に使用するのが「多重比較」です。
(組み合わせのそれぞれにt検定を行うようなものですが、t検定を繰り返すと有意基準を達成してしまうことがあるので、ここではその影響を取り除いた検定である多重比較を使用します)
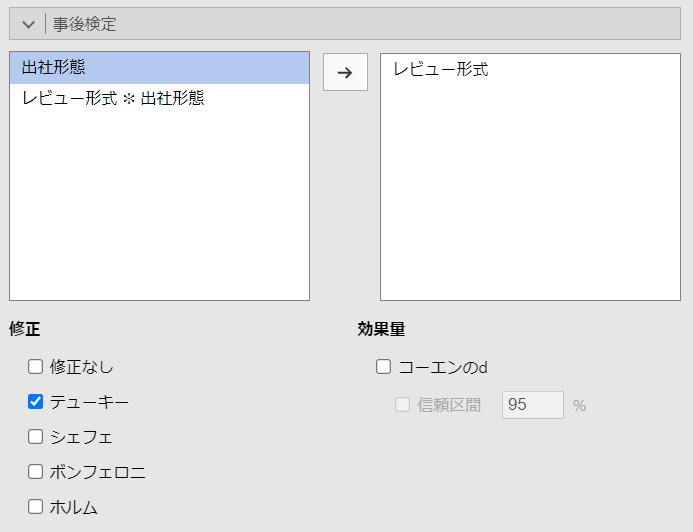
事後検定の設定を以下のように設定します。
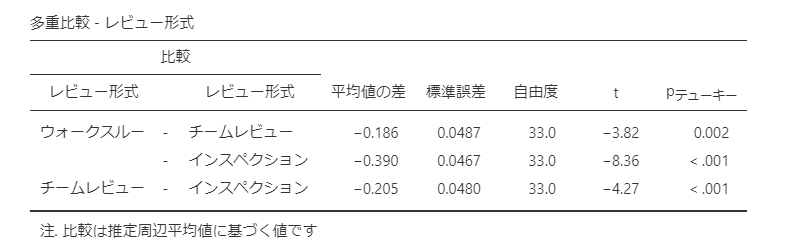
検定結果が以下のように表示されました。
レビュー形式の組み合わせについて、今回の例ではどの組み合わせでもp値は有意(5%以下)であることがわかります。
このように多重比較を使うことで、どの組み合わせが有意であって、どの組み合わせが有意でないか、について分析をすることができます。
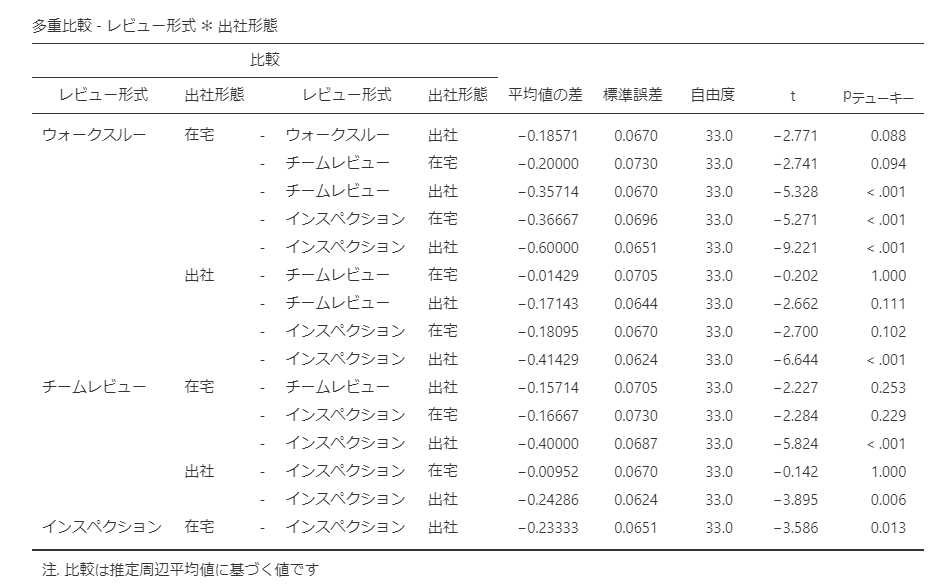
今回は交互作用「レビュー形式*出社形態」に有意差が無かったので事後検定を実施しませんでしたが、事後検定を実施した場合は以下のように表示されます。
交互作用の組み合わせは上図のように多くの組み合わせがあります。
中には有意水準を満たしているものも見えますが、全体としては否定されているので、ここでは深く追求しないでおきます。
まとめ
#分散分析は交互作用も判断できる優れた手法です。
やはりデータがあると効果の説明に説得力が出ます。
ただし、どの分析手法にも当てはまりますが、要因・水準の取り方を誤ると「関係ない」と思われていた事柄を「関係あり」としてしまうことや、逆に「関係がある」のに「無関係」としてしまうこともあります。
要因の設定、水準の設定をどのようにするかについては、皆様の各職場で試行錯誤する必要があると思いますが、使いこなせれば強力なツールになることは間違いないでしょう。
よろしければ他のブログ記事も参照ください。
データ分析に活用して頂ければ幸いです。
注意)オンプレミス版のjamoviで分散分析がうまく動作しなかったのでクラウド版を使用しました。