ロボットマニピュレータ制御のアルゴリズム3

(株)豆蔵　エンジニアリングソリューション事業部　石井隆寛

1. はじめに

（株）豆蔵では様々なロボット技術を開発している。他社製ロボットを用いてクライアントの要望に応える応用技術を開発することが多いが、自社でも6軸や7軸のアームを持つ産業用ロボット、いわゆるロボットアーム＝マニピュレータを一から開発している。この開発を通じて様々な応用技術や提案を生み出している。今回ここで得た知見を読者の方と共有したいと思う。本解説では6軸の産業用垂直多関節型マニピュレータを例にしてこれを制御するさまざまなしくみを説明したい。

今回は、これまで説明してきた軌跡生成処理アルゴリズムを適用してマニピュレータ＝ロボットアームを動作させたとき、必ず問題となる「特異点」について理論も含めて解説する。また、その解決方法、いわゆる「特異点回避」の方法の一例を紹介する。

2. ロボットアームの特異点

特異点とは？

これまで述べてきたようにロボットアームは6個の関節軸を動かすことにより様々な姿勢をとり、ツール先端（TCP=Tool Center Point ）の位置や姿勢（向き、方向）を変えることができる。しかしある特定の姿勢に近づく、あるいはそれから遠ざかるとき、突然一部のアームが急激な動作をしてサーボモータや減速機に過大な負荷をかけたり、大きな振動を生じさせたりすることがある。その特定の姿勢状態をロボットアームの「特異点」と呼ぶ。本稿で取り上げている6軸の産業用垂直多関節型マニピュレータの場合、経験的に下記の3つの特異点が知られている。

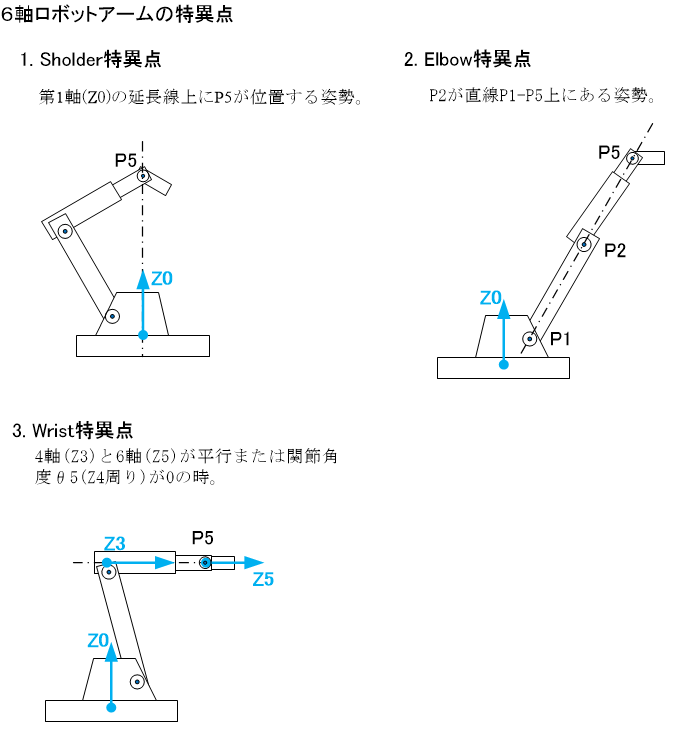
Shoulder特異点
Elbow特異点
Wrist特異点

下記のようなマニピュレータのジオメトリにおいて、（※Z軸は各関節での回転軸）

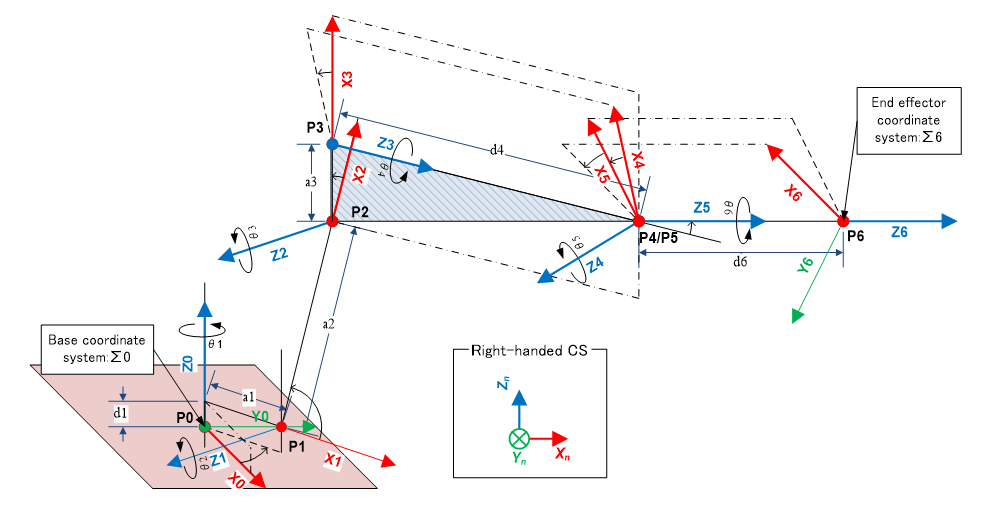
これら3つの特異点は下記のように定義されている。

これらの特異点の姿勢に近くなると、アームの動きに不都合が生じる。例えば、「3.Wrist特異点」の姿勢からTCPの向きは変えないようZ4軸（Bn軸）方向（この絵では紙面の裏から表方向）にゆっくりと移動させると、P3とP4の間のアームがZ3軸（Rt軸）周りに急激に回転する。この回転角度は一瞬で90度近くになる。このときP3より先にある部材はかなりの重量があるのでRt軸のサーボモータに急激な負荷がかかり、場合によっては大きな振動を発生することがある。

特異点の数学的説明

以上のような特異点とは一体何なのか、数学的に説明してみよう。

まず、以前説明した「速度の順運動学/逆運動学計算」に関する記述で紹介したヤコビ行列とその利用方法を再掲する。

$\vec{P_t}$ ：TCP位置
$\vec{P_0}$ ：ベース座標系原点位置
” $\times$ "はベクトル積
右肩のＴは行列の転置を表す。

J=\left( \begin{array}{ccccc} [\vec{Z_0} \times (\vec{P_t}-\vec{P_0})]^T & [\vec{Z_1} \times (\vec{P_t}-\vec{P_1})]^T & [\vec{Z_2} \times (\vec{P_t}-\vec{P_2})]^T & ... &[\vec{Z_5} \times (\vec{P_t}-\vec{P_5})]^T\\ \vec{Z_0}^T & \vec{Z_1}^T & \vec{Z_2}^T & ... & \vec{Z_5}^T\\ \end{array} \right)

このヤコビ行列を用いて下記のように関節軸速度からTCPの並進速度と回転速度が計算できる。

\vec{v}=J \vec{\omega}

また下記のように逆の変換もできる。

\vec{\omega} =J^{-1} \vec{v}

ここで

$\vec{\omega}$ :各関節軸の角速度を表す6次元縦ベクトル
$\vec{v}$ :TCPの速度を表す6次元縦ベクトル

であり、より具体的には

$\omega_i$ ：{ ${i=1,2,\cdots,6}$ } ：各関節軸での角速度
$\vec{v_t}$ ：TCPの3次元並進速度ベクトル $(v_{tx},v_{ty},v_{tz})$
$\vec{w_t}$ ：TCPの3次元回転速度ベクトル $(w_{tx},w_{ty},w_{tz})$

とすると

\vec{\omega}= ( \omega_1, \omega_2 , \omega_3 , \omega_4 , \omega_5 , \omega_6 ) ^T

\vec{v}= \left( \begin{array}{c} {\vec{v_t}^T} \\ {\vec{w_t}^T} \\ \end{array} \right)

と表される。

このヤコビ行列 $J$ はロボットアームの瞬間的な姿勢で決まるが、これの逆行列 $J^{-1}$ が求まらないことがある。このときTCPの瞬間的な移動量 $\vec{v}$ がどうであれ、関節軸の瞬間的な回転量 $\vec{\omega}$ が不定となる。そもそも逆行列の要素を求めるときは、行列式の値で割る操作が必要なので $J^{-1}$ が求まらないということは行列式が0つまり、

\rm{det}[J] = 0

と同義である。これがまさに特異点をとる姿勢である。一方、特異点近くの姿勢においては、その行列式 $\rm{det}[J]$ は0に近いが0ではない。そのため一応 $J^{-1}$ は求まる。しかしその要素は微小の $\rm{det}[J]$ で割ったものであるため巨大な数値になりえる。そのため

\vec{\omega} =J^{-1} \vec{v}

を計算すると、TCPの移動量 $\vec{v}$ が小さくても関節角度の変化量 $\vec{\omega}$ の要素も巨大となりえる。これが特異点近傍で一部のアームが異常な動作を引き起こす理由である。

特異点回避

主な回避方法

以上のように特異点付近では動作に問題があるため、これらの特異点を何とか回避する方法が考えられてきた。主に以下の方法がある。

特異点に近づくと本来の軌跡（TCPの経路や向き）をやや変える。
特異点に近づくと本来の軌跡を変えないよう全モータの速度を一律に急速に落とす。

上記1.の方法では事前に計画した動作時間通り動く半面、本来の軌跡から逸脱するため精度が損なわれる。また2.の方法では計画通りの正確な軌跡をたどれるが、事前に予定した時刻よりかなり遅れた動作になってしまう。

さて、産業用ロボットマニピュレータは、工場などの生産現場で使用されることが多いため、時間節約の問題は重要である。また、精度が要求される重要な軌跡では特異点にならないよう、また単なるツールの移動場面でのみ特異点になるよう、注意してプログラミングすれば、1.の方法で構わない。そのため本稿では実際に採用した1.の方法の一例である「特異点低感度運動分解」を利用した特異点回避の方法を説明する。（参考文献1.参照）

特異点低感度運動分解による特異点回避

方法の概要

参考文献1.は、特異点に近づいた時本来の軌跡（TCPの経路や向き）をやや変えるための低感度運動分解行列 $J^{*}$ を導入する方法である。パラメータで細かくその変え方（感度）を調整することも可能である。この方法を6軸マニピュレータに適用した場合の具体的計算方法を説明する。なお、当該文献では任意の多関節マニピュレータに関して一般的な言及をしており、必ずしも $J$ が正方行列とは限らないため $J^{-1}$ の代わりに一般化逆行列（疑似行列）に置き換えて議論されている。しかし、本稿では $J$ や $J^{-1}$ が正方行列であるので、そのまま置き換えずに利用する。

さて、本方法の概要は次のようになる。

正確なTCPの位置と姿勢との誤差を最小にするための条件から、低感度運動分解を行うための低感度運動分解行列 $J^{*}$ が導出できる。これを $J^ {-1}$ の代りに軌跡生成時に用いれば、特異点付近において、TCPの「姿勢」精度を犠牲にする一方、TCPの「位置」精度は保つような動作をさせることができる。その結果、無事に特異点を回避することができる。このとき、どの関節軸も思わぬ急加速はせず滑らかに作動する。ちなみに $J^{*}$ は特異点近傍から遠ざかると完全に $J^{-1}$ と一致する。

特異点低感度運動分解行列 $J^*$

導出は省き、結果である低感度運動分解行列 $J^{*}$ の定義を以下に示す。

J^{*}=N_{\theta}^{-1}\hat{J}^{T}(\hat{J}\hat{J}^{T} + kI)^{-1}N_{r}

ここで

\begin{align*} & \hat{J}= N_r J N_{\theta}^{-1}\\ & k=k_f(k_0, w_0, w_f(J)) \\ & w_f(J)=|\rm{det}[J]| \end{align*}

また、

$N_θ$ $N_{θ}$ :関節軸の運動の感度を決める6x6の対角行列
- デフォルト値： $\rm{diag}(1,1,1,1,1,1)$
$N_r$ $N_{r}$ :TCPの運動の感度を決める6x6の対角行列
- デフォルト値： $\rm{diag}(a,a,a,b,b,b)$
- ここで $a=1/V_{max},\quad b=1/W_{max}$
- $V_{max}$ ：設計仕様上のTCP最高並進速度
- $W_{max}$ ：設計仕様上のTCP最高回転速度
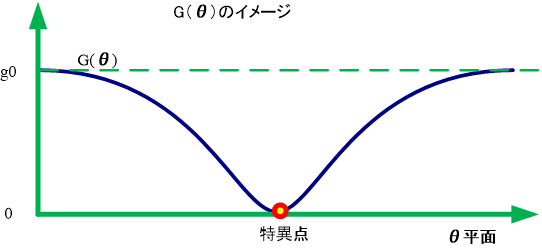
$k$ $k$ ：ロボットアームの姿勢が特異点に近いかどうかの中村の指標
- 特異点で $k_0$ 、特異点から離れると0に漸近
- 下記が定義

k=k_f(k_0,w_0,w) = \left \{ \begin{array}{} k_0(1-|w/w_0|)^2 & \rm{if}(|w/w_0|<1) \\ 0 & \rm{else} \end{array} \right.

下記が上記関数 $k_f()$ のグラフ概形（横軸： $w$ , 縦軸： $k$ ）

ここで $k_0$ と $w_0$ は制御調整値であり下記指針で決める。

$k_0$
- 0.0～1.0で調整可能。デフォルト値：0.01
- 大きくすると特異点近傍でTCPの移動量に対する $θ$ の感応性が小さくなる。また一部の軸の急加速回転は緩和するが、目標軌道からは逸脱しやすくなる。
- 小さくすると目標軌道への追従が良くなる。
$w_0$
- 特異点領域と非特異点領域をわける境界基準値
- $w_0=w_f(J_0)$ で算出。この行列 $J_0$ はWrist特異点姿勢（ $θ_5$ =0°）を基準として、 $θ_5$ =10°～30°くらいに変更したときの姿勢に対して算出されたヤコビ行列を使用するとよい。

$J^{*}$ を利用した軌跡生成アルゴリズム

$J^{*}$ を利用して特異点回避可能な軌跡生成を行う具体的な方法について説明する。

はじめに、ある関節角度セット $\vec{\theta_\tau}$ で構成される姿勢に対して、算出される $J^*$ を

J^{*}=J^*(\vec{\theta_\tau})

と関数表現する。
また、 $t$ を時刻として、

$\vec{\theta}_{(t)}$ ：取るべき関節角度の時系列
$\vec{v}_{(t)}$ ：TCPの速度を表す6次元縦ベクトルの時系列
$\Delta t$ ：微小時間

とすると、理論的には下記のような積分を含む漸化式

\vec{\theta}_{(t+\Delta t)}=\int_{\tau=t}^{t+\Delta t}{J^*(\vec{\theta}_{(\tau)})\vec{v}_{(\tau)}}d\tau + \vec{\theta}_{(t)}

を計算すれば、時々刻々と関節角度セットが出力され、特異点回避可能な軌跡生成が可能となる。しかしながら実際には、 $\vec{v}_{(t)}$ を正確に算出することは困難である。仮に本来軌跡（これまで述べてきた軌跡生成方法によって算出した軌跡）から算出した本来速度 $\vec{v}^O_{(t)}$ を $\vec{v}_{(t)}$ であると見なして上記積分を行い新たな $\vec{\theta}_{(t)}$ を得たとしても、特異点付近を通過するごとに本来コースからどんどん外れることとなる。

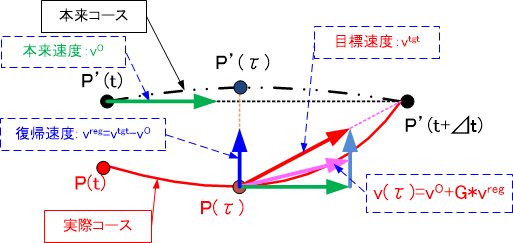
例えば下記の図のように実際コースの $P(\tau)$ にいるとき、本来コースだと取るべき速度(本来速度)、 $\vec{v}^{O}$ で動いてしまうと、そのままずれっぱなしで移動するので次時点には予定の目標点 $P'(t+\Delta t)$ からさらに離れてしまう。これを避けるためには予定コースにちょうど戻るための復帰速度 $\vec{v}^{reg}$ 分偏向させつつ移動すればよい。なお $\vec{v}^{reg}$ は現時点から正確に目標点へ移動するための目標速度 $\vec{v}^{tgt}$ と本来速度 $\vec{v}^{O}$ との差である。

以上のような概念のもと、本来コースから外れても必ず戻れるよう、以下のようなフィードバック制御を使った計算を行う。

まず、 $\vec{v}_{(\tau)}$ を下記のように定義する。

\vec{v}_{(\tau)}=\vec{v}^{O}_{(\tau)} + G(\vec{\theta}_{(\tau)}) \vec{v}^{reg}_{(\tau)}

ここで、 $\tau$ は時刻 [ $t$ ～ $t+\Delta t$ ]の間の時刻であり、 $FK(\vec{\theta})$ を関節角度からTCPの座標を求める操作、つまり順運動学の操作を表す関数とすると、

\vec{v}^{tgt}_{(\tau)}=\frac{FK(\vec{\theta}^{O}_{(t+\Delta t)})-FK(\vec{\theta}_{(\tau)})}{t+\Delta t - \tau}

\vec{v}^{O}_{(\tau)}=\frac{FK(\vec{\theta}^{O}_{(t+\Delta t)})-FK(\vec{\theta}^{O}_{(t)})}{\Delta t}

\vec{v}^{reg}_{(\tau)}=\vec{v}^{tgt}_{(\tau)}-\vec{v}^{O}_{(\tau)}

G(\vec{\theta})=g_0 \left( \frac{1-k_f(k_0,w_0,w_f(J(\vec{\theta})))}{k_0} \right) ^{\rho}

この中で、 $\vec{v}^{O}_{(\tau)}$ は本来コースの上をTCPが動作している時の速度であり、 $\vec{v}^{tgt}_{(\tau)}$
はTCPが現状から真っすぐ次の本来位置/姿勢に向かうための目標速度であり、 $\vec{v}^{reg}_{(\tau)}$ はTCPを本来コースに近づけるための復帰速度である。また、

$G(\vec{\theta}）$ は、目標TCP軌道に復帰するGain値（0.0～1.0)。特異点近傍ではGが0に近づく。
$\rho$ は2.0とする。
$g_0$ は回復係数。デフォルト値：0.0001
$\Delta t$ は軌跡生成のサンプル時間と同じにする。

以上を用いて先の積分を計算すれば良い。しかし実際はこの積分を簡単化した下記の近似を使うことができる。これによって本来コースに復帰できる関節角度セットが時々刻々と出力できる。

\vec{\theta}_{(t+\Delta t)}={J^*(\vec{\theta}_{(t)})\vec{v}_{(t)}}\Delta t + \vec{\theta}_{(t)}

なお、特異点を通過する場合は直線的コースを期待しても少しコースが横ずれしてしまうことがある。この場合は $k_0$ 、 $w_0$ の値または $V_{max}$ 、 $W_{max}$ の値を調整することによりコースのずれを調整できる。また $g_0$ の値が大きいとコースが振動することに注意されたい。

3. 終わりに

ロボットアームの特異点とは何か、また6軸ロボットアームでの特異点回避方法について解説した。実際のシステム実装では、これらを実機で動作させてみてパラメータ調整を行う。また実用的には、ペンダントを使ったJOG操作時の特異点回避機能や特異点検知アラーム機能なども別途必要である。しかしこれらは本稿の理論の応用で実装可能である。

参考文献

中村仁彦, 花房秀郎、「関節形ロボットアームの特異点低感度運動分解」, 計測自動制御学会論文集第20巻第5号 ( 昭和59年5月 )
遠山茂樹 (著)、　「ロボット工学 (メカトロニクス教科書シリーズ)」、コロナ社 (1994)
以上