Let's Simulate the Boid Model with PyGame
Back to TopTo reach a broader audience, this article has been translated from Japanese.
You can find the original version here.
Introduction
#Do you know about the boid model, an artificial life model? When we hear "artificial life," it sounds like creating life using advanced technology, but upon research, it seems to be a simulation that reproduces the movement of birds.
And it seems like it can be done with relatively simple programming!
Real birds have brains, so it's just reproducing their movement, but I thought I'd give it a try and this time, based on the following literature, I simulated the boid model with PyGame.
The logic is almost (or exactly?) the same, but since I couldn't find any nice Japanese literature on PyGame (as far as I searched), I'm introducing it here as a note to myself.
I hope you'll read to the end.
What is the Boid Model?
#The boid model is an artificial life model devised and created by Craig Reynolds, an American animation programmer. "Boids" is a coined term meaning "bird-like," and it is an algorithm that can create flocks from the following three simple rules:
- Cohesion: Move towards the center of the flock
- Separation: Keep a distance to avoid collisions
- Alignment: Move in the same direction as the surrounding birds
By combining these rules, the birds on the computer move in an amazingly natural way.
After Reynolds' proposal, various improvements have been made to the boid model to produce more complex and lifelike movements. For example, models that incorporate emotions like fear when forming flocks or models that introduce the power to avoid danger from external threats, where a bird sensing danger becomes the leader and steers the flock away from harm, have been proposed.
This time, we simply reproduced the model with the above three rules added.
Simulating the Boid Model with PyGame
#First, let's move them freely.
#First, let's move a flock of birds freely without setting any rules.
The directory structure is as follows:
boid/
│ main.py
└───model
__init__.py
bird.py
main.py is the executable file, and bird.py is the class file for a single bird. bird.py defines the initial values and behavior rules for individual birds.
The source codes are as follows:
import pygame
import random
import numpy as np
RANGE_OF_DIRECTIONS = [0, 360]
BIRD_COLORS = [
'#FFA5CC', # pink
'#80FF25', # green
'#A0D4FF', # skyblue
]
class Bird:
def __init__(self, bird_id, width, height):
self.bird_id = bird_id
self.width = width
self.height = height
self.direction = random.uniform(
np.radians(RANGE_OF_DIRECTIONS[0]),
np.radians(RANGE_OF_DIRECTIONS[1])
) # Random initial angle
# Position and velocity vector
self.position = np.array([random.uniform(0, width), random.uniform(0, height)])
self.velocity = np.array([np.cos(self.direction), np.sin(self.direction)])
# Acceleration vector
self.acceleration = np.array([0, 0])
self.acceleration_to_cohere = np.array([0, 0])
self.acceleration_to_separate = np.array([0, 0])
self.acceleration_to_align = np.array([0, 0])
# Bird's shape
self.polygon = np.array([(20, 0), (0, 5), (0, -5)])
self.type_id = self.bird_id % 3
self.color = BIRD_COLORS[self.type_id]
def move(self):
self.position += self.velocity
# If the bird hits a wall, it passes through to the opposite side
if self.position[0] > self.width or self.position[0] < 0:
self.position[0] = np.abs(self.position[0] - self.width)
if self.position[1] > self.height or self.position[1] < 0:
self.position[1] = np.abs(self.position[1] - self.height)
def display(self, screen):
# Forming the rotation matrix
rotation_matrix = np.array([[np.cos(self.direction), -np.sin(self.direction)],
[np.sin(self.direction), np.cos(self.direction)]])
# Rotate to make the head face the direction of movement.
rotated_polygon = np.dot(self.polygon, rotation_matrix.T) + self.position
pygame.draw.polygon(screen, self.color, rotated_polygon, 0)
import pygame
import numpy as np
from model.bird import Bird
# Total number of flock
BIRD_NUM = 100
# Main execution
def main():
pygame.init()
# Setting the screen size
width, height = 800, 600
screen = pygame.display.set_mode((width, height))
pygame.display.set_caption("Boid Simulation")
# Generating birds
bird_list = []
for i in range(BIRD_NUM):
bird_list.append(Bird(i, width, height))
clock = pygame.time.Clock()
# Execution
while True:
for event in pygame.event.get():
if event.type == pygame.QUIT:
pygame.quit()
exit()
# Movement of each bird
for bird in bird_list:
# Action
bird.move()
screen.fill((0, 0, 0))
# Drawing birds
for bird in bird_list:
bird.display(screen)
pygame.display.flip()
clock.tick(30)
if __name__ == '__main__':
main()
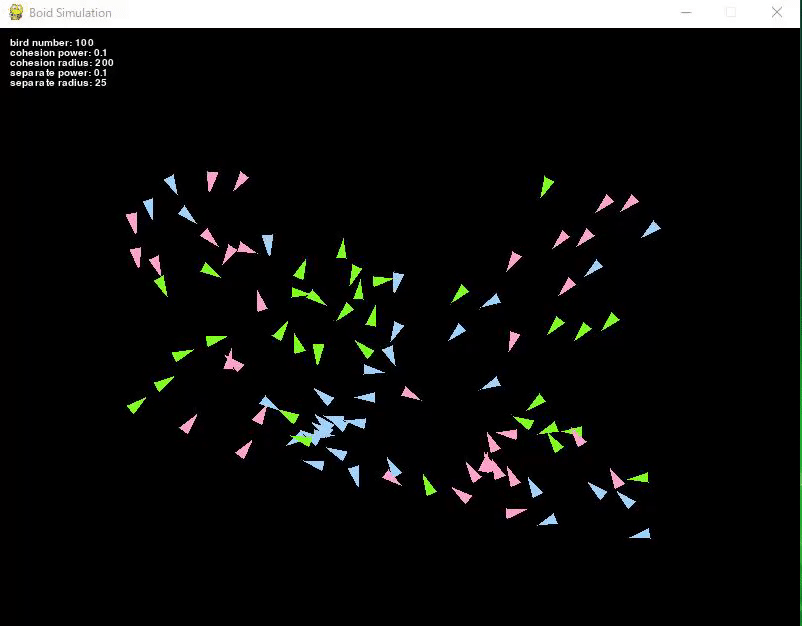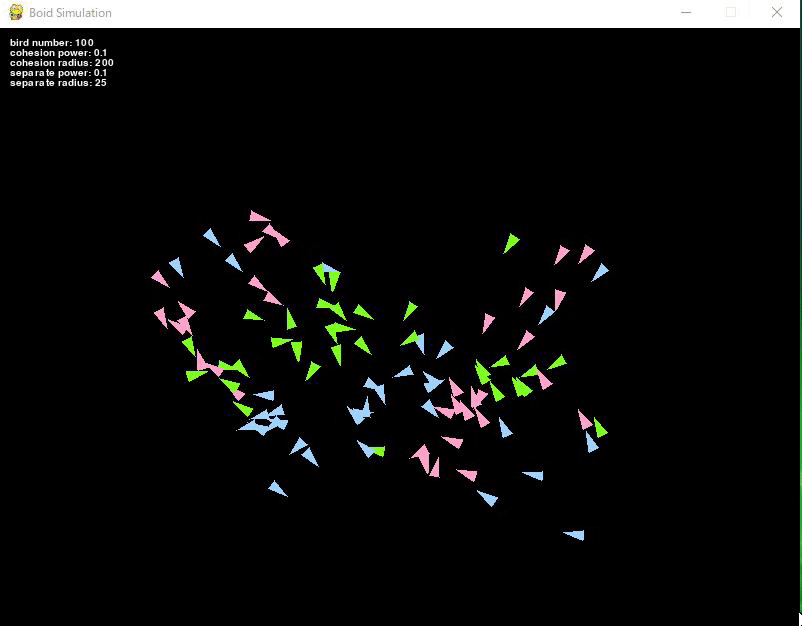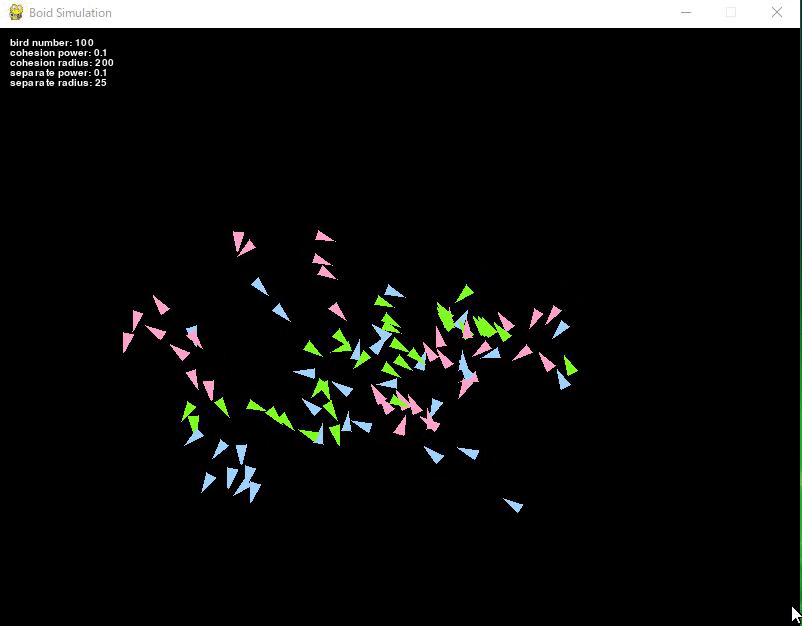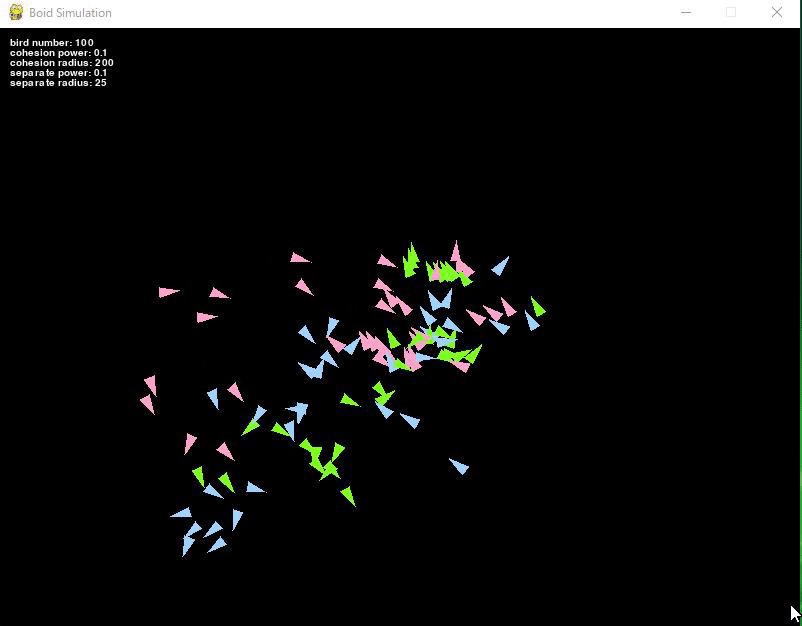
100 birds were prepared, and their initial positions and directions were set randomly.
Also, as a trial, the birds were color-coded into three types.
The birds continue to move in the direction determined at the beginning.
In this state, the birds do not interfere with each other, so they move in any direction they like.
By the way, they are implemented to appear on the opposite side when they pass through a wall.
Here are the execution results.
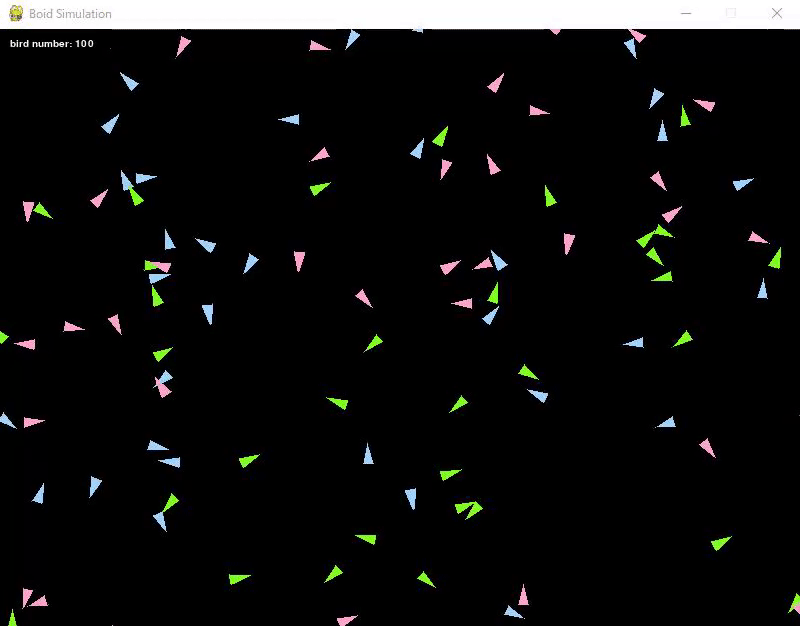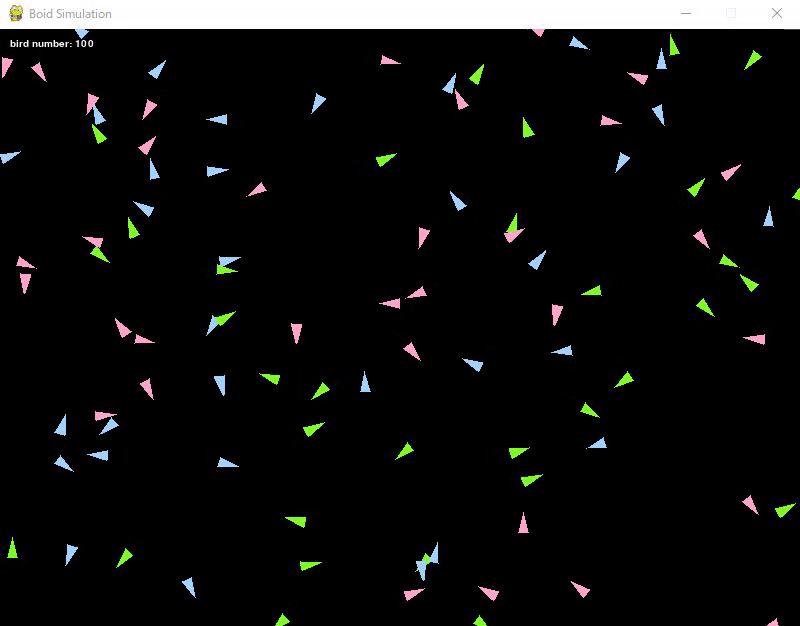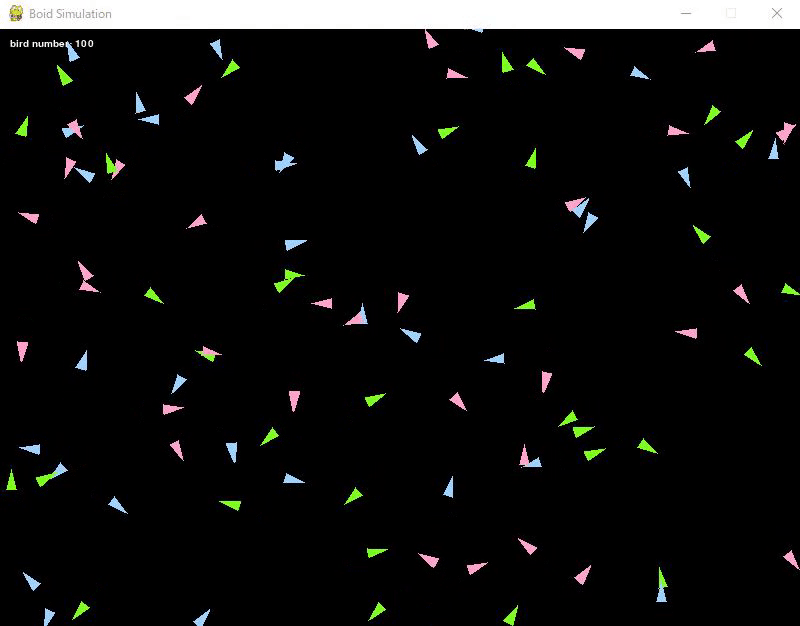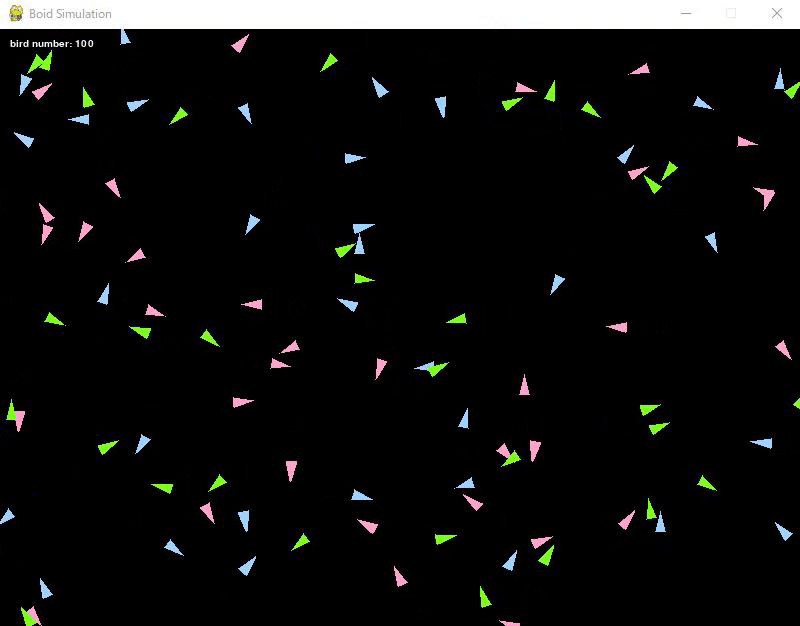
Adding the Cohesion Rule
#Next, let's add only the cohesion rule.
When cohering, we set how much radius the birds within cohere (RADIUS_OF_COHERE) and the force towards the flock (POWER_OF_COHERE).
Since it's almost the same as the above source code, I'll spare you the details and only show the added parts.
class Bird:
# Modify the move method
def move(self):
# Calculate the acceleration vector.
self.acceleration = self.acceleration_to_cohere + self.acceleration_to_separate + self.acceleration_to_align
# Calculate the direction of movement from the sum of the acceleration and velocity vectors.
vector = self.velocity + self.acceleration
self.velocity = (vector) / np.linalg.norm(vector)
self.direction = np.arctan2(self.velocity[1], self.velocity[0])
self.position += self.velocity
# If the bird hits a wall, it passes through to the opposite side
if self.position[0] > self.width or self.position[0] < 0:
self.position[0] = np.abs(self.position[0] - self.width)
if self.position[1] > self.height or self.position[1] < 0:
self.position[1] = np.abs(self.position[1] - self.height)
# Cohesion rule
def cohere(self, bird_list, distance_l, power, radius):
# Extract nearby flock
near_bird_ids = [
d[1] for d in distance_l[self.bird_id]
if 0 < d[0] < radius and bird_list[d[1]].color == self.color]
if len(near_bird_ids) > 0 :
near_bird = [bird_list[bird_id] for bird_id in near_bird_ids]
# Center of gravity vector of nearby flock
center_of_near = np.mean(np.array([bird.position for bird in near_bird]))
# Difference between self and center of gravity vector of the flock
vector = np.subtract(center_of_near, self.position)
# Calculate acceleration towards the center of gravity vector of the flock
self.acceleration_to_cohere = power * (vector/np.linalg.norm(vector))
else:
self.acceleration_to_cohere = np.array([0,0])
# Adding initial values
# Cohesion rule
POWER_OF_COHERE = 0.1
RADIUS_OF_COHERE = 200
# Main execution
def main():
# Omitted
# Execution
while True:
# Omitted
# Distance and direction between two birds
distances_list = distances_of_vectors([bird.position for bird in bird_list]) # Added
# Movement of each bird
for bird in bird_list:
# Cohesion
bird.cohere(bird_list, distances_list, POWER_OF_COHERE, RADIUS_OF_COHERE) # Added
# Action
bird.move()
# Omitted
# Method added
# Generate a two-dimensional list storing distances between vectors
# Each element (i,j) of the matrix stores the distance between vector[i] and vector[j] and the index of vector[j].
def distances_of_vectors(vectors):
vector_num = len(vectors)
distance_list = [[0] * vector_num for _ in range(vector_num)]
for i in range(vector_num):
distance_list[i][i] = (0, i)
for j in range(vector_num):
if i < j:
# Calculate the distance between two vectors.
distance = np.linalg.norm(np.subtract(vectors[i], vectors[j]))
# Store the calculated distance at index i,j.
distance_list[i][j] = (distance, j)
distance_list[j][i] = (distance, i)
return distance_list
This time, by adding the cohesion rule, birds of the same color cohere together.
The bird's speed changes direction due to acceleration, causing birds of the same color to cohere.
Adding the Separation Rule
#When only the cohesion rule was added, the flock became too small and densely packed.
Therefore, we add a separation rule to prevent overcrowding.
The separation rule is similar to the cohesion rule, setting how much radius birds separate (RADIUS_OF_SEPARATION) and the force to move away from the flock (POWER_OF_SEPARATION).
class Bird:
# Adding the separation rule
def separate(self, bird_list, distance_l, power, radius):
# Extract nearby flock
near_bird_ids = [
d[1] for d in distance_l[self.bird_id]
if 0 < d[0] < radius]
if len(near_bird_ids) > 0 :
near_bird = [bird_list[bird_id] for bird_id in near_bird_ids]
# Center of gravity vector of nearby flock
center_of_near = np.mean(np.array([bird.position for bird in near_bird]))
# Difference between self and center of gravity vector of the flock
vector = np.subtract(center_of_near, self.position)
# Calculate acceleration to move away from the center of gravity vector of the flock
self.acceleration_to_separate = - power * (vector/np.linalg.norm(vector))
else:
self.acceleration_to_separate = np.array([0,0])
# Adding initial values
# Separation rule
POWER_OF_SEPARATE = 0.1
RADIUS_OF_SEPARATE = 25
# Main execution
def main():
# Omitted
# Execution
while True:
# Omitted
# Movement of each bird
for bird in bird_list:
# Cohesion
bird.cohere(bird_list, distances_list, POWER_OF_COHERE, RADIUS_OF_COHERE)
# Separation
bird.separate(bird_list, distances_list, POWER_OF_SEPARATE, RADIUS_OF_SEPARATE) # Added
# Action
bird.move()
# Omitted
The logic is almost the same as the cohesion rule, extracting birds of the same color within a certain radius and calculating the acceleration from their current position.
The difference from the cohesion rule is that a minus sign is added when calculating acceleration, making the bird move away from the flock.
This makes the bird move in the opposite direction away from the flock.
Finally, we'll add the "alignment rule."
Adding the Alignment Rule
#class Bird:
# Adding the alignment rule
def align(self, bird_list, distance_l, power, radius):
# Extract nearby flock
near_bird_ids = [
d[1] for d in distance_l[self.bird_id]
if 0 < d[0] < radius and bird_list[d[1]].color == self.color]
if len(near_bird_ids) > 0 :
near_bird = [bird_list[bird_id] for bird_id in near_bird_ids]
# Determine the direction of the flock
vector = np.sum([bird.velocity for bird in near_bird], axis=0)
# Calculate acceleration to align with the flock's direction
self.acceleration_to_align = power * (vector/np.linalg.norm(vector))
else:
self.acceleration_to_align = np.array([0,0])
# Adding initial values
# Alignment rule
POWER_OF_ALIGN = 0.1
RADIUS_OF_ALIGN = 100
# Main execution
def main():
# Omitted
# Execution
while True:
# Omitted
# Movement of each bird
for bird in bird_list:
# Cohesion
bird.cohere(bird_list, distances_list, POWER_OF_COHERE, RADIUS_OF_COHERE)
# Separation
bird.separate(bird_list, distances_list, POWER_OF_SEPARATE, RADIUS_OF_SEPARATE)
# Alignment
bird.align(bird_list, distances_list, POWER_OF_SEPARATE, RADIUS_OF_SEPARATE) # Added
# Action
bird.move()
# Omitted
Adding the alignment rule made the movement even more natural.
The alignment rule is about moving in the same direction as the flock of birds within a certain radius.
Since the rule is applied to each color group, the blue, green, and pink groups align and fly in their respective directions.
(Note: The video is short, so it may not look aligned, but if you leave it for a while, you can see them aligning and flying.)
Conclusion
#This time, we conducted a simple boid model simulation using PyGame.
The boid model seems to have various applications and has seven parameters, so adjusting each parameter allows for various experiments.
Personally, it would be interesting to extend this model by placing food, setting breeding and lifespan, or combining it with a genetic algorithm for simulation.
Finally, I'll introduce the complete source code with all three rules added.
Please give it a try.
Source Code
#- Directory structure
boid/
│ main.py
└───model
__init__.py
bird.py
- Complete source code
import pygame
import random
import numpy as np
RANGE_OF_DIRECTIONS = [0, 360]
BIRD_COLORS = [
'#FFA5CC', # pink
'#80FF25', # green
'#A0D4FF', # skyblue
]
class Bird:
def __init__(self, bird_id, width, height):
self.bird_id = bird_id
self.width = width
self.height = height
self.direction = random.uniform(
np.radians(RANGE_OF_DIRECTIONS[0]),
np.radians(RANGE_OF_DIRECTIONS[1])
) # Random initial angle
# Position and velocity vector
self.position = np.array([random.uniform(0, width), random.uniform(0, height)])
self.velocity = np.array([np.cos(self.direction), np.sin(self.direction)])
# Acceleration vector
self.acceleration = np.array([0, 0])
self.acceleration_to_cohere = np.array([0, 0])
self.acceleration_to_separate = np.array([0, 0])
self.acceleration_to_align = np.array([0, 0])
# Bird's shape
self.polygon = np.array([(20, 0), (0, 5), (0, -5)])
self.type_id = self.bird_id % 3
self.color = BIRD_COLORS[self.type_id]
def move(self):
# Calculate the acceleration vector.
self.acceleration = self.acceleration_to_cohere + self.acceleration_to_separate + self.acceleration_to_align
# Calculate the direction of movement from the sum of the acceleration and velocity vectors.
vector = self.velocity + self.acceleration
self.velocity = (vector) / np.linalg.norm(vector)
self.direction = np.arctan2(self.velocity[1], self.velocity[0])
self.position += self.velocity
# If the bird hits a wall, it passes through to the opposite side
if self.position[0] > self.width or self.position[0] < 0:
self.position[0] = np.abs(self.position[0] - self.width)
if self.position[1] > self.height or self.position[1] < 0:
self.position[1] = np.abs(self.position[1] - self.height)
# Cohesion rule
def cohere(self, bird_list, distance_l, power, radius):