【夏休みの自由研究】人工生命による生態系シミュレーションで、生命の絶滅を回避する方法を模索してみた
Back to Topはじめに
#世間は夏休み!!
皆様いかがお過ごしでしょうか?
学生の方は、宿題は完璧でしょうか?
私は「宿題は夏休み最終日まで放置する派」のため、ギリギリで焦って一夜漬けで何とか終わらせる、というのを何度も繰り返した記憶があります。
もう二度とやるか、と反省してものど元過ぎれば何とやら。一年後にはまたやってしまう、というのが人間の性ですね……!
とはいえ、一夜漬けでなかなか終わらせることができないものもあります。
それが「夏休みの自由研究」!
テーマ決めから、実験、考察、それをレポートにまとめる、という果てしない作業。
なかなか一日でやりきるのは難しい宿題です。
そんな悩める学生の皆様の一助となれば、と今回はパソコン1台あればできる人工生命による生態系のシミュレーションを作ってみました。
より具体的には、ボイドモデルといって鳥の動きをシミュレーションするプログラムを発展させて、食事・繁殖・寿命などの設定を新たに追加してシミュレーションをしてみました。
基本的なボイドモデルに関する詳しい内容は下記リンクで紹介しています。
「PyGameでボイドモデルのシミュレーションをしよう」
ボイドモデルの3つの基本的なルールから鳥の群れの動きをPyGameで再現してみました。
今回はこの記事で紹介した内容を発展させて、シミュレーションをしています。
繁殖をする際には、いわゆる遺伝的アルゴリズムという手法を用いて、出来るだけ長く生き永らえるように人工生命を最適化してみました。
まずはボイドモデルについて簡単に復習した後に、ボイドモデルやモデルを動かす環境にどういう設定を追加したのか紹介します。
その後、実際に適用してみたシミュレーションを実施し、どういう挙動をしたのか、どのパラメータがどう最適化されたのかご紹介します。
ソースコードはGitHubで公開していますので、ぜひそちらも見ていただければ幸いです。
ボイドモデル
#ボイドモデルは、アメリカのアニメーション・プログラマであるクレイグ・レイノルズが考案・作成した人工生命モデルです。「ボイド(Boids)」とは、bird-old、つまり「鳥っぽいもの」を意味する造語で、以下の3つの簡単なルールから群れを作り出すことができるアルゴリズムです。
- 集合(cohesion):群れの中心に向かう
- 分離(separation):ぶつからないように距離を取る
- 整列(alignment):周りの鳥の動きと同じ方向に動く
これらルールを組み合わせることで、コンピュータ上の鳥たちは驚くほど自然な動きをします。
実際にシミュレーションしてみると、以下のように集合・分離・整列をして動く人工生命のシミュレーションができます。
※図や映像はクリックで拡大します。
しかしこのアルゴリズムにはまだ改善できそうな部分があります。
まず、これらのルールはあくまで「群れの動き」の再現に過ぎないということです。
実際の鳥は、餌を食べたり、寿命があったり、繁殖したりします。
より実際の鳥に近い生態系シミュレーションするならば、そういうルールや定義を追加する必要があります。
またこのモデルでは、恣意的に設定しなければならないパラメータがルールごとに複数あります。
例えば集合ルールでは、群れの中心に向かうための力(上図のcohesion power)と鳥が集合する範囲(上図のcohesion radius)を設定しています。
分離ルールでも、整列ルールでも同様で、ルールを追加するごとに設定するパラメータが増えていきます。
このパラメータは自分で調整する必要があって、自然に決まったパラメータではありません。
最適な鳥の動きを再現するために、人間が手でパラメータを設定するのは少々不自然な気が個人的には感じます。
ボイドモデルに追加した設定
#というわけで、実際の鳥に近いシミュレーションをするために、今回は以下の設定をシミュレーションに追加してみました。
- 体力・寿命
- 餌の探索・食事
- 繁殖
体力・寿命
#まずボイドモデルに体力や寿命を設定してみました。
鳥の動きに速さのパラメータを追加し、その速さで動くたびに体力が削られるように設定しています。
鳥の動きが速すぎるとその分体力が減り、逆に遅いと体力の減りが遅くなります。
体力が0になると、鳥は死亡してしまいます。
例えば、初期の体力を500、鳥の速さを20とすると、体力は20ずつ減り消耗を抑えられますが動きは緩慢です。
逆に速さを50にすると、速く動ける代わりに体力が50ずつ減っていくので、あっという間に体力がなくなり最終的に死亡します。
次に寿命ですが、鳥はサイクルを迎えるたびに寿命を消費するように設定しています。
これは速さや動きには関係なく、体力が有り余っていても寿命を迎えると死亡します。
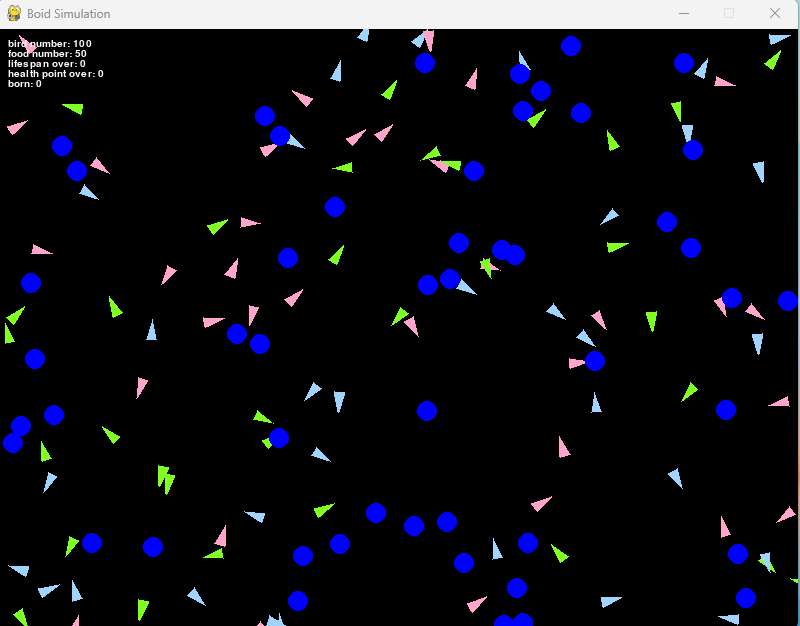
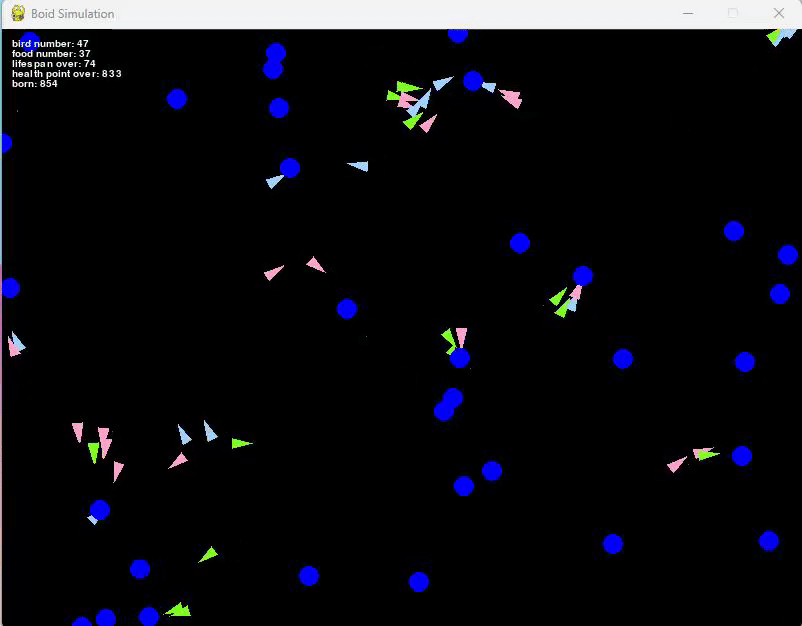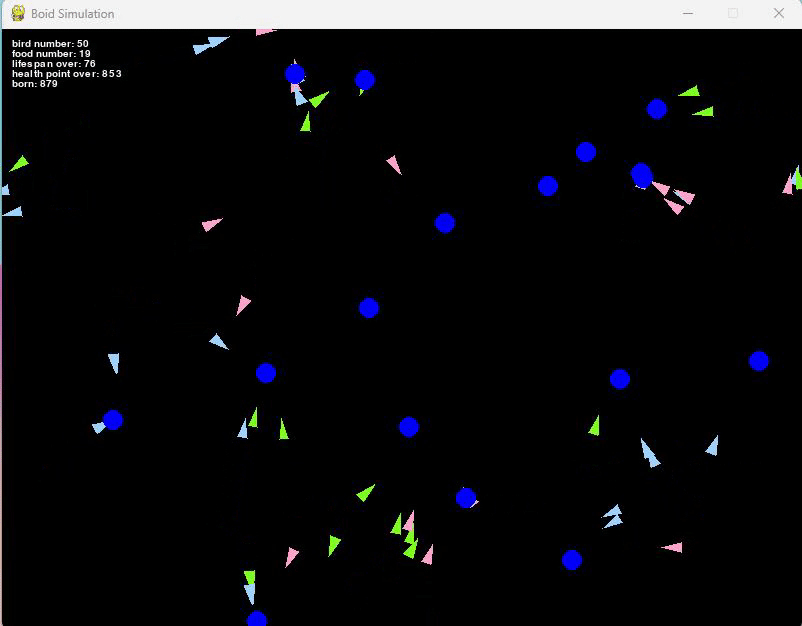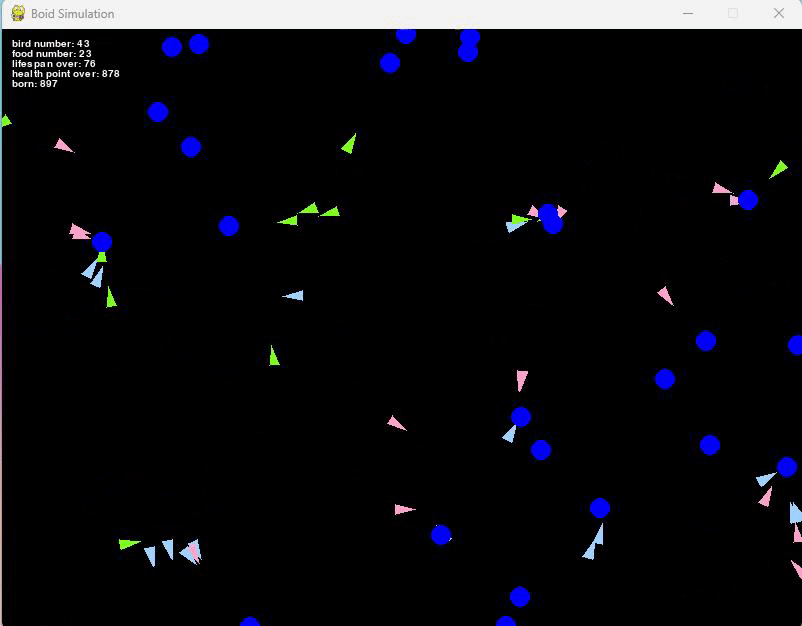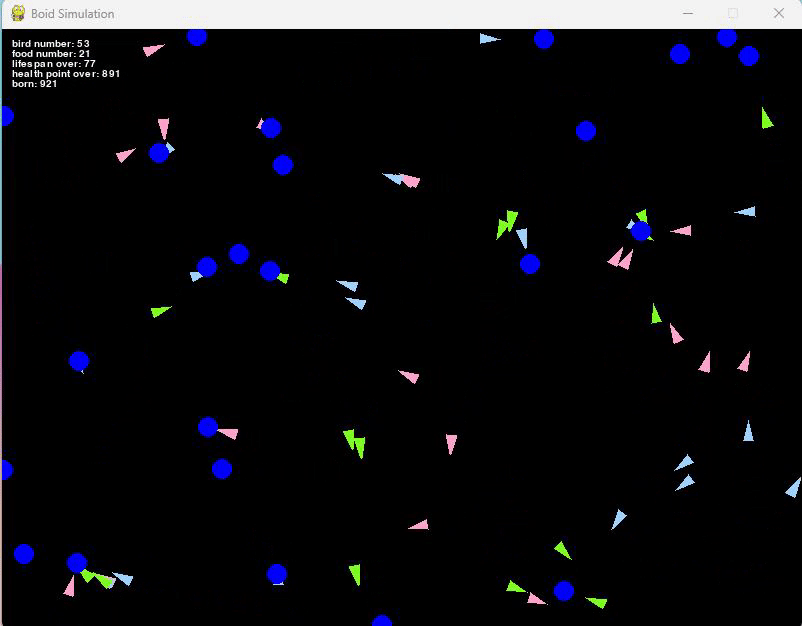
実際に体力や寿命を設定したシミュレーションが以下となります。
| 速さ:20 | 速さ:50 |
|---|---|
 |
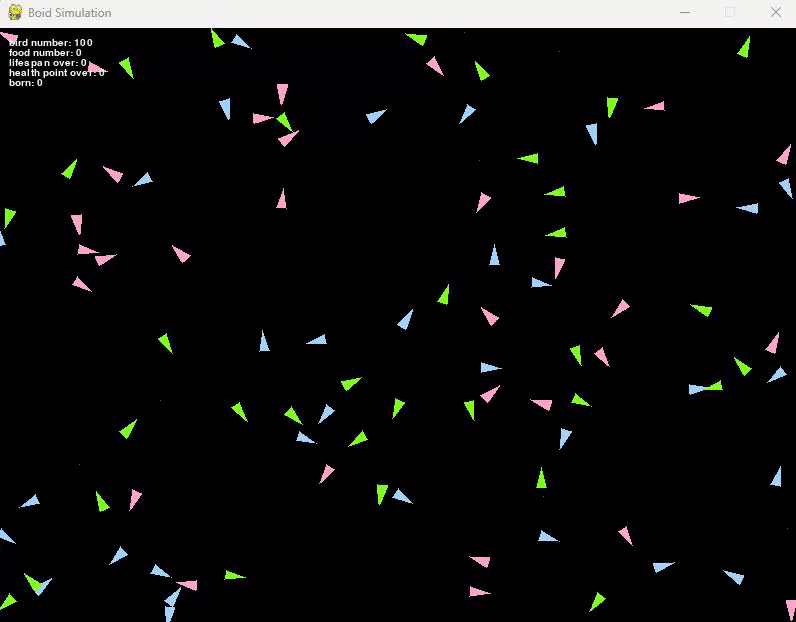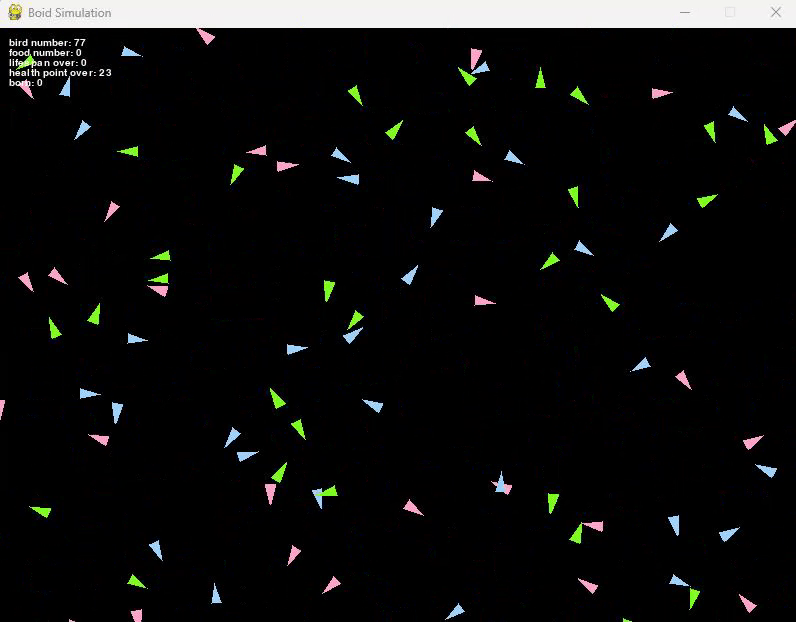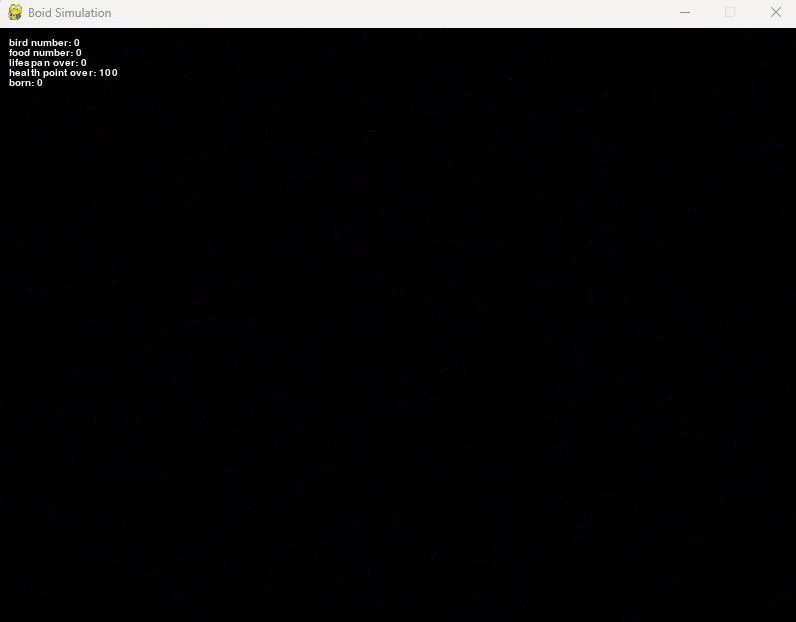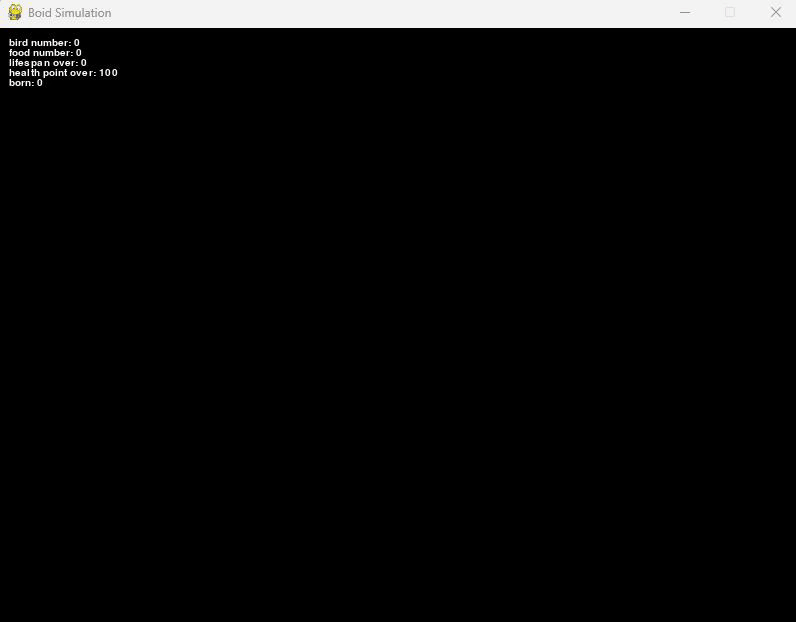 |
左図が速さ20で動く鳥たちのシミュレーション、右図が速さ50で動く鳥たちです。
体力は500~1000の間でランダムに設定しています。
右図の方が速く動いているので、あっという間に絶滅しているのがわかりますね。
このシミュレーションを見ていると、ほとんどの鳥たちは回復する手立てがないので寿命を迎える前に体力が尽きて死亡してしまいます。
そのため次に餌を配置して、鳥の体力を回復させ生存期間を延ばすように設定してみましょう。
餌の探索・食事
#鳥たちが食事をするためには、餌の概念をこの環境に入れる必要があります。
そのため餌モデルを新たに作成しました。
import pygame
import random
FOOD_POWER = 150
RADIUS_OF_FOOD = 10
# 餌
class Food:
def __init__(self, x, y, food_power=FOOD_POWER):
self.x = x
self.y = y
self.food_power = food_power
self.food_radius = RADIUS_OF_FOOD
self.eaten = False
def move(self):
pass
def display(self, screen):
pygame.draw.circle(screen, (0, 0, 255), (int(self.x), int(self.y)), RADIUS_OF_FOOD)
FOOD_POWERは餌が持っているエネルギーで、鳥が餌を食べるとFOOD_POWER分だけ回復します。
RADIUS_OF_FOODは餌の大きさとしています。
餌モデルは、画面上にランダムで生成されるようにしました。
また餌が食べられたら、ある一定の確率で新たに餌が生えてくるように設定してみました。
あまりおいしくなさそうですが、上図の青丸を餌としています。
鳥は餌に近づくと餌を食べる(食事ルール)ように設定し、
また集合ルールを応用して鳥が餌を追いかけるルール(餌の探索ルール)も追加しました。
具体的に、餌の探索ルールについては以下のように設定しています。
- 鳥を中心にある半径以内の餌を探す。
- その中で鳥に最も近い餌を選択する。
- 最も近い餌に向かうように加速度ベクトルを計算する。
- 集合・分離・整列のルールで計算した加速度ベクトルと合成して、群れを成しつつ餌を追いかけるように進行方向を求める。
食事ルールはもっと単純で、
- 鳥が餌の位置(+ 餌の大きさも加味する)に行くと餌を食べる。
- 食べられた餌は環境から消去する。
- 餌が食べられると、ある確率で餌が生えてくる。
という風にルールを追加しました。
この2つのルールを加えたシミュレーションが以下となります。
餌の探索ルールと食事ルールを追加したことで体力の消耗による死は少なくなりましたが、寿命があるため個体数は徐々に減っていき全滅してしまいました。
最後の設定として、絶滅を回避するために繁殖ルールを追加してみましょう。
繁殖
#餌の探索ルールや食事ルールを追加しても、鳥には寿命があるため、個体数が徐々に減っていってしまいます。
そうならないためには、一定確率で鳥を新たに生み出す必要があります。
実際の鳥は2匹の鳥が交配して子供を産むので、それに倣って繁殖ルールを以下のように設定してみました。
- 鳥を中心にある半径以内の群れを探す。
- その中で自分の親以外の最も体力が高い鳥を選択する。
- 2匹の鳥の体力を200減らす(※交配や出産には体力が必要なため)。
- 子供を生成する。
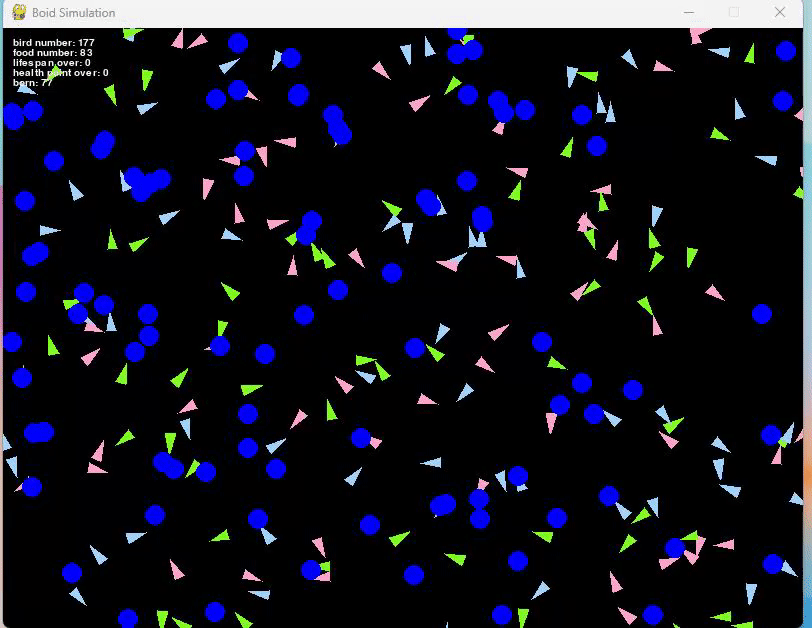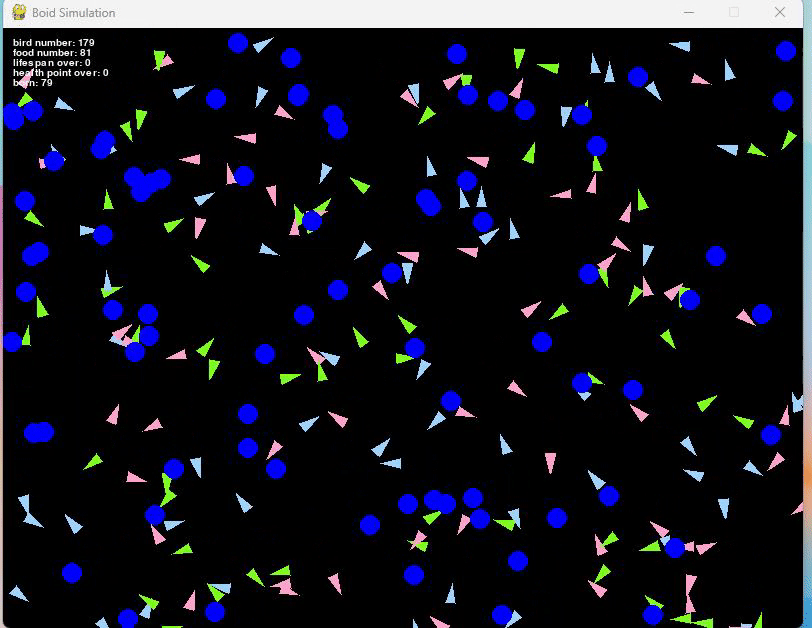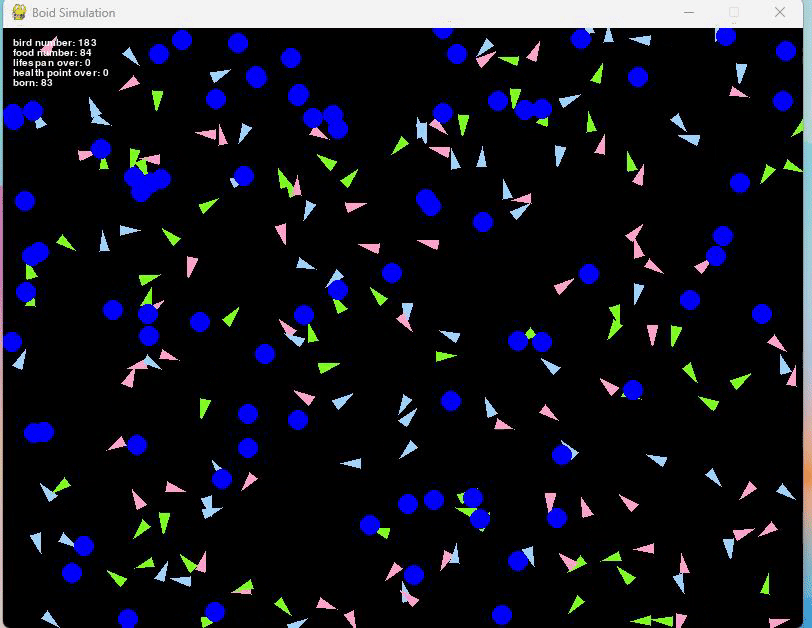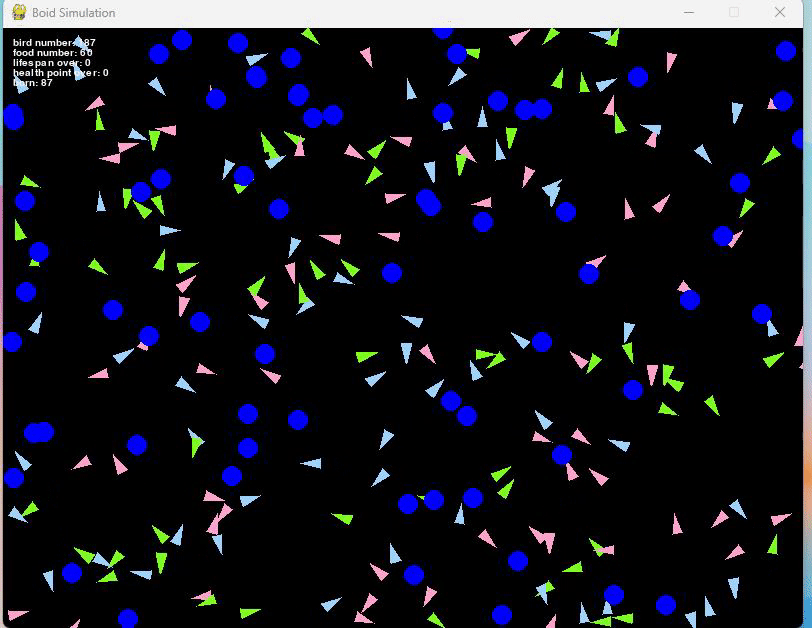
このルールを加えたシミュレーションが以下となります。
短い動画だと少しわかりにくいかもしれませんが、左上にあるbornと表示されている部分が徐々に増えているのがわかると思います。
これは生まれた鳥の総数を表しています。
この繁殖ルールを追加したことで、死亡と繁殖が繰り返されるようになり、餌の数や初期の鳥の総数などパラメータを微調整することで、安定した集団を作ることも可能となりました。
パラメータの最適化をするために
#ここまで数々のルールを追加していきましたが、これらのルールを増やすごとに調整しなければならないパラメータが増えていきました。
| ルール | パラメータ | 説明 |
|---|---|---|
| 集合 | POWER_OF_COHERE | 群れの中心に向かうための力 |
| RADIUS_OF_COHERE | 集合ルールを適用する対象(群れ)を探す範囲 | |
| 分離 | POWER_OF_SEPARATE | 群れの中心から離れるための力 |
| RADIUS_OF_SEPARATE | 分離ルールを適用する対象(群れ)を探す範囲 | |
| 整列 | POWER_OF_ALIGN | 群れの移動方向と同じ方向に整列するための力 |
| RADIUS_OF_ALIGN | 整列ルールを適用する対象(群れ)を探す範囲 | |
| 餌の探索 | POWER_OF_FOOD | 餌に向かうための力 |
| RADIUS_OF_FOOD | 餌を探索する範囲 | |
| 繁殖 | RADIUS_OF_BORN | 繁殖するための鳥を探す範囲(鳥の交配範囲) |
| 体力 | HEALTH_POINT | 鳥の体力 |
| BIRD_SPEED | 鳥の速さ。鳥が速く動くたびに体力が減っていく | |
| 寿命 | LIFESPAN_POINT | 鳥の寿命 |
ルールと各パラメータを列挙すると、以上のようにかなり多くのパラメータを定義することになってしまいました。
絶滅を回避して安定した集団を作るには、これらのパラメータを人が手で調整する必要があり、やや不自然に感じてしまいます。
そこで自然にパラメータを最適化するためのアルゴリズムを「繁殖ルール」に追加しましょう。
いわゆる「遺伝的アルゴリズム」というものですが、本格的にするには適合度の計算などより複雑なアルゴリズムとなります。
そのためここではかなり簡易的なアルゴリズムでシミュレーションしているというのに注意してください。
この最適化のアルゴリズムを追加して、以下のように繁殖ルールを設定してみました。
- 鳥を中心にある半径以内の群れを探す。
- その中で自分の親以外の最も体力が高い鳥を選択する。
- 2匹の鳥の体力を200減らす(※交配や出産には体力が必要なため)。
- 各パラメータに対して、体力が高い方のパラメータを採用する(交叉)。← ★追加部分
- 採用したパラメータに対して、一定確率で値をランダムにして返却する(突然変異)。← ★追加部分
- 返却したパラメータを子供のパラメータとして定義。← ★追加部分
- 子供を生成する。
また最初に生成する鳥たちは各パラメータに対してランダムな値を持つことにしました。
ただし体力と寿命に関しては、固定としました。
最適化するとその分絶滅を回避する確率があがりそうですが、
今回は動きに関するパラメータの最適化を目的とするため、このように設定しました。
import pygame
import random
import numpy as np
RANGE_OF_DIRECTIONS = [0, 360]
BIRD_COLORS = [
'#FFA5CC', # pink
'#80FF25', # green
'#A0D4FF', # skyblue
]
# -----------------------------------------
# パラメータをランダムに生成する場合の最大値/最小値
# 遺伝的アルゴリズムを利用する場合(IS_USE_GA = Trueの場合)利用します。
# -----------------------------------------
# 動きの速さ
BIRD_SPEED = 20
# 集合ルール
POWER_OF_COHERE = 1000
RADIUS_OF_COHERE = 300
# 分離ルール
POWER_OF_SEPARATE = 1000
RADIUS_OF_SEPARATE = 300
# 整列ルール
POWER_OF_ALIGN = 1000
RADIUS_OF_ALIGN = 300
# 繁殖ルール
RADIUS_OF_BORN = 300
# 食事ルール
POWER_OF_FOOD = 1000
RADIUS_OF_FOOD = 300
# HP
HEALTH_POINT = 500
# 寿命の最大値
LIFESPAN_POINT = 1000
# 突然変異ルール
MUTATION_RATE = 0.01
MUTATION_POWER_RATE = 2
MUTATION_RADIUS_RATE = 2
#
# -----------------------------------------
#
# 鳥モデル
class Bird:
def __init__(self,
bird_id,
width,
height,
parent_bird_ids= None,
type_id=None,
speed_param = None,
cohere_param = None,
separate_param = None,
align_param = None,
food_param = None,
born_param = None,
position = None,
health_point = HEALTH_POINT,
lifespan = None,
generation_id = None
):
self.bird_id = bird_id
self.width = width
self.height = height
self.parent_bird_ids = parent_bird_ids if parent_bird_ids is not None else []
self.generation_id = generation_id if generation_id is not None else 1
# 初期値
self.speed_param = speed_param if speed_param is not None else random.randint(0, BIRD_SPEED)
self.cohere_param = cohere_param if cohere_param is not None else (random.uniform(0, POWER_OF_COHERE), random.randint(0, RADIUS_OF_COHERE))
self.separate_param = separate_param if separate_param is not None else (random.uniform(0, POWER_OF_SEPARATE), random.randint(0, RADIUS_OF_SEPARATE))
self.align_param = align_param if align_param is not None else (random.uniform(0, POWER_OF_ALIGN), random.randint(0, RADIUS_OF_ALIGN))
self.born_param = born_param if born_param is not None else (1, random.randint(0,RADIUS_OF_BORN))
self.food_param = food_param if food_param is not None else (random.uniform(0, POWER_OF_FOOD), random.randint(0, RADIUS_OF_FOOD))
# ランダムな初期の角度
self.direction = random.uniform(
np.radians(RANGE_OF_DIRECTIONS[0]),
np.radians(RANGE_OF_DIRECTIONS[1])
)
# 位置と進行方向ベクトル
self.position = position if position is not None else np.array([random.uniform(0, width), random.uniform(0, height)])
self.velocity = np.array([np.cos(self.direction), np.sin(self.direction)])
# 加速度ベクトル
self.acceleration = np.array([0, 0])
self.acceleration_to_cohere = np.array([0, 0])
self.acceleration_to_separate = np.array([0, 0])
self.acceleration_to_align = np.array([0, 0])
self.acceleration_to_food = np.array([0, 0])
# 鳥のHP
self.health_point = health_point
# 鳥の寿命
self.lifespan = lifespan if lifespan is not None else random.randint(200, LIFESPAN_POINT)
# 鳥の形状
self.polygon = np.array([(20, 0), (0, 5), (0, -5)])
self.type_id = type_id if type_id else self.bird_id % 3
self.color = BIRD_COLORS[self.type_id]
#
# 省略
#
# 繁殖ルール
def born(self, last_index, bird_list, distance_l, is_use_ga):
power, radius = self.born_param
near_birds = self.get_near_bird_list(bird_list, distance_l, radius, True)
near_birds_without_parent = [bird for bird in near_birds if self.bird_id not in bird.parent_bird_ids]
child_bird = None
if self.health_point > 500 and len(near_birds_without_parent) > 0:
# HPが最も高い鳥を選択する
pair_bird = max(near_birds_without_parent, key=lambda bird: bird.health_point)
pair_bird_index = next((i for i in range(len(bird_list)) if bird_list[i].bird_id == pair_bird.bird_id), -1)
if pair_bird.health_point < 500 or pair_bird_index == -1:
return None
# 両親のhealth_pointを減らす
self.health_point -= 200
pair_bird.health_point -=200
# 交叉と突然変異による子供のパラメータ生成
def blend_param(param1, param2):
if is_use_ga:
# 体力がある方のパラメータを優先して返します。
if self.health_point >= pair_bird.health_point:
return param1
else:
return param2
# 両親の平均を取る場合はこちらを利用してみてください。
# return (param1[0] + param2[0]) / 2 , round((param1[1] + param2[1]) / 2)
else:
# 遺伝的アルゴリズムを利用しないため、自身のパラメータを返します。
return param1
def mutate_param(param):
if is_use_ga and random.uniform(0, 1) <= MUTATION_RATE:
print("occur mutation")
return (random.uniform(0, param[0] * MUTATION_POWER_RATE), random.randint(0, param[1] * MUTATION_RADIUS_RATE))
return param
child_speed_param = mutate_param(blend_param((0, self.speed_param), (0, pair_bird.speed_param)))[1]
child_cohere_param = mutate_param(blend_param(self.cohere_param, pair_bird.cohere_param))
child_separate_param = mutate_param(blend_param(self.separate_param, pair_bird.separate_param))
child_align_param = mutate_param(blend_param(self.align_param, pair_bird.align_param))
child_food_param = mutate_param(blend_param(self.food_param, pair_bird.food_param))
child_born_param = mutate_param(blend_param(self.born_param, pair_bird.born_param))
# 子供の初期位置
child_position = np.array([random.uniform(0, self.width), random.uniform(0, self.height)])
# 子供の世代数
child_generation_id = max(self.generation_id, pair_bird.generation_id) + 1
# 子供を生成します
child_bird = Bird(
bird_id=last_index + 1,
width=self.width,
height=self.height,
parent_bird_ids=[self.bird_id, pair_bird.bird_id],
speed_param=child_speed_param,
cohere_param=child_cohere_param,
separate_param=child_separate_param,
align_param=child_align_param,
born_param=child_born_param,
food_param=child_food_param,
position=child_position,
generation_id=child_generation_id
)
bird_list.append(child_bird)
bird_list[pair_bird_index] = pair_bird
print("child born")
return child_bird
#
# 省略
#
こうすることによって、より体力が高い(つまり死ににくい)個体が自然と増えていきます。
実際にシミュレーションすると、最初のうちは体力がなくなりすぐ死ぬ個体もいましたが、
次第に体力を保つために餌を追いかける力が強くなっているのがわかります。
また繁殖も頻繁に行っているようですので、個体数も50匹前後で安定しているようです。
ただし餌の初期個数を10個、新しく生まれる餌を5個、餌が生まれる確率を50%としています。
餌の初期値や生まれる餌を増やせば、もっと個体数が多くなるはずです。
例えば、餌の初期個数を20個、新しく生まれる餌を10個、餌が生まれる確率を50%とすると、
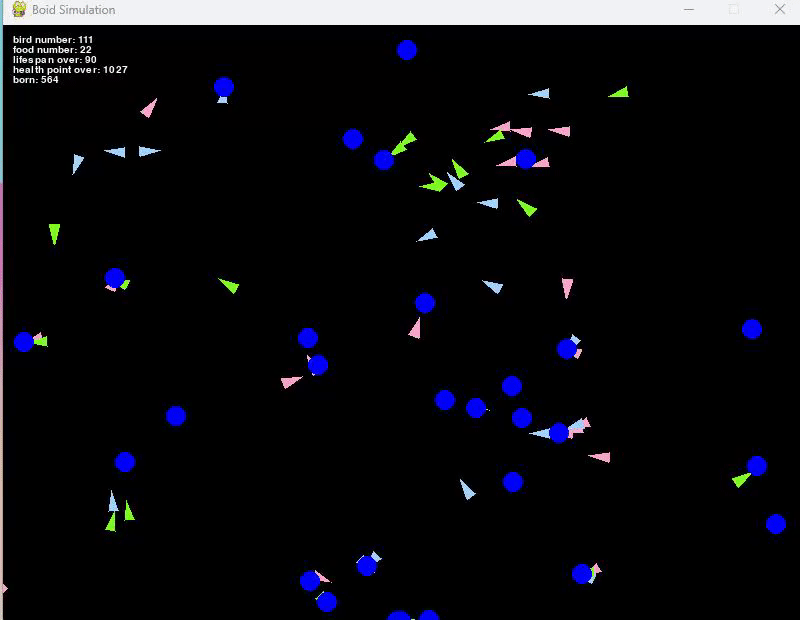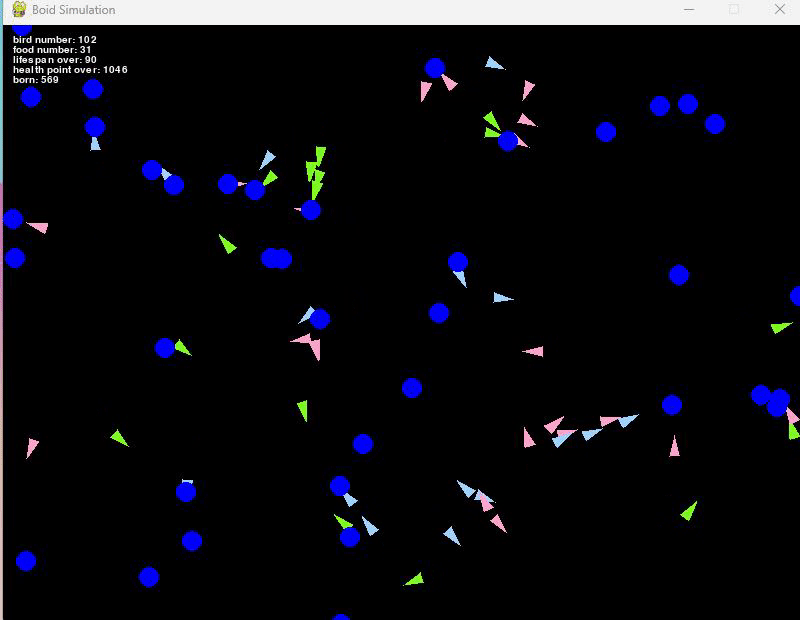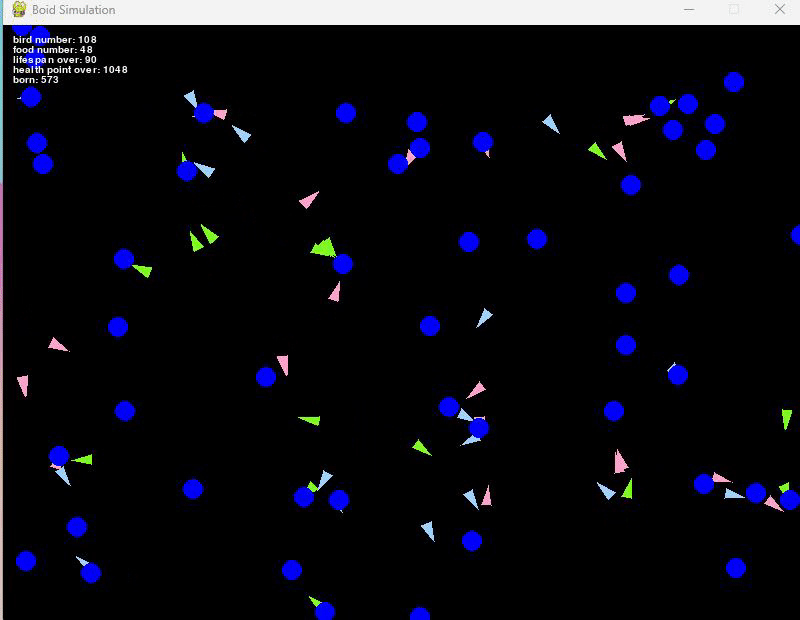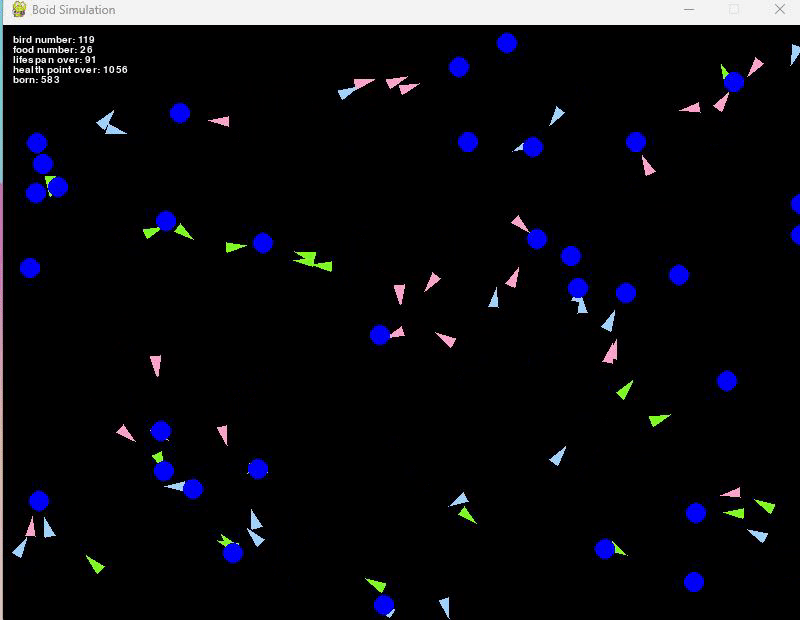
だいたい100匹前後で安定している集団となりました。
たまに鳥が増えすぎることで餌が枯渇し、一気に減少して20匹くらいになることも観察できましたが、それもまた生物っぽいです。
生態系シミュレーションの結果
#では具体的にパラメータがどうなっていったのかを見ていきましょう。
ここでは、初期値を以下のように設定しました。
- 鳥の初期個数:100匹
- 餌の初期個数:10個
- 新しく生まれる餌:10個
- 餌が生まれる確率:50%
この初期値でだいたい10000匹くらい生まれるまでシミュレーションしてみました。
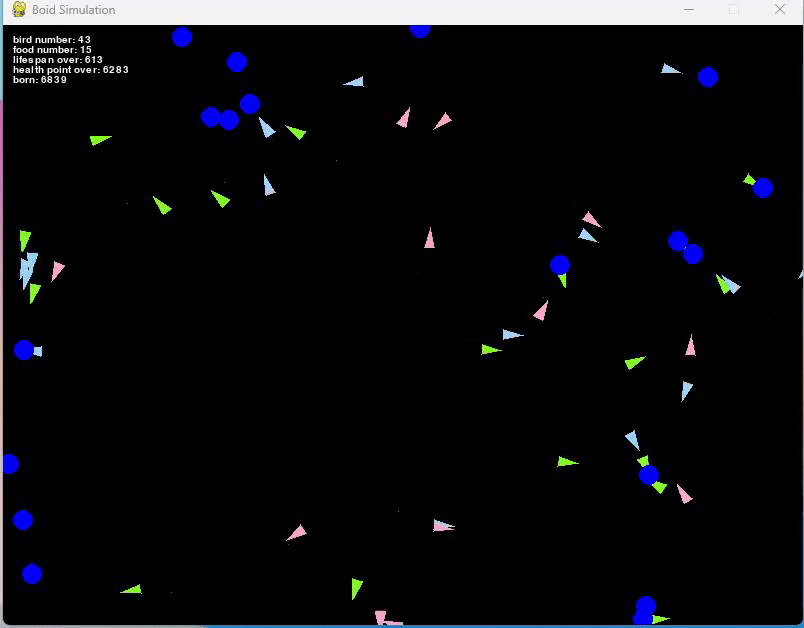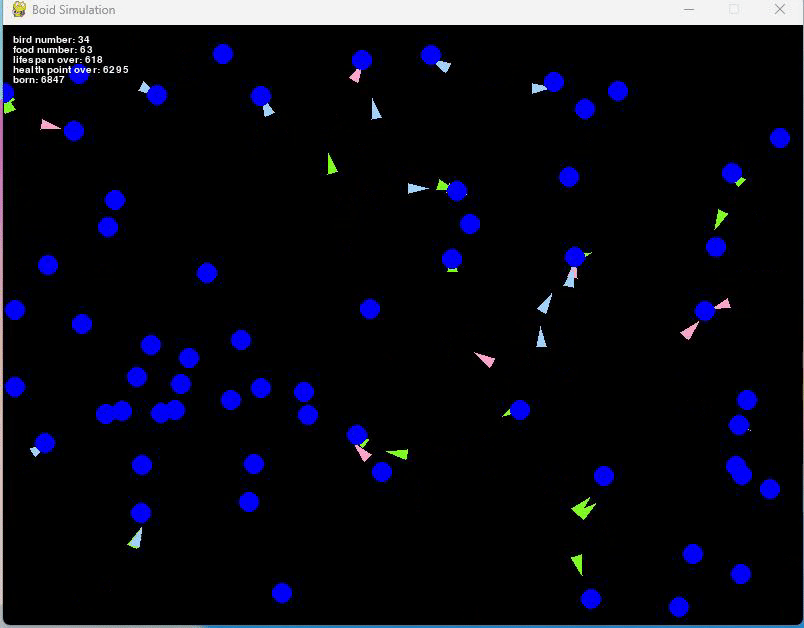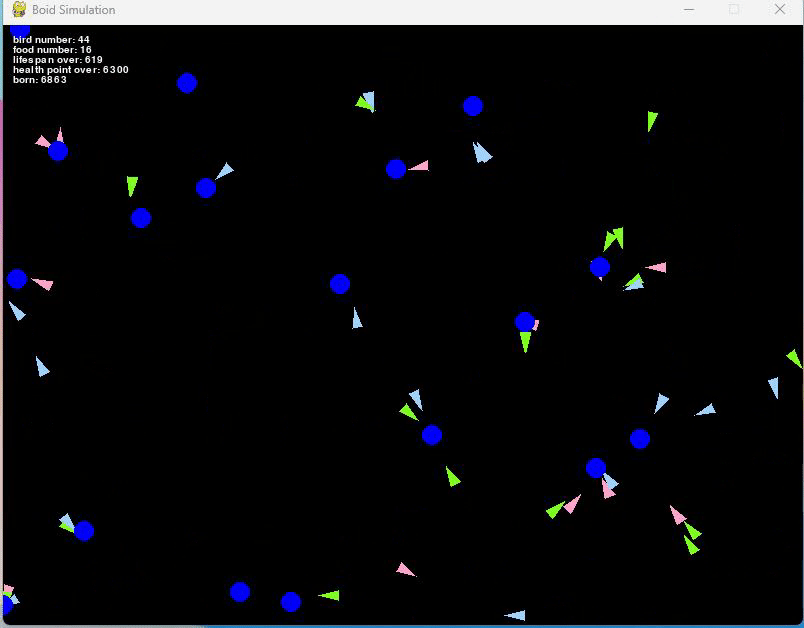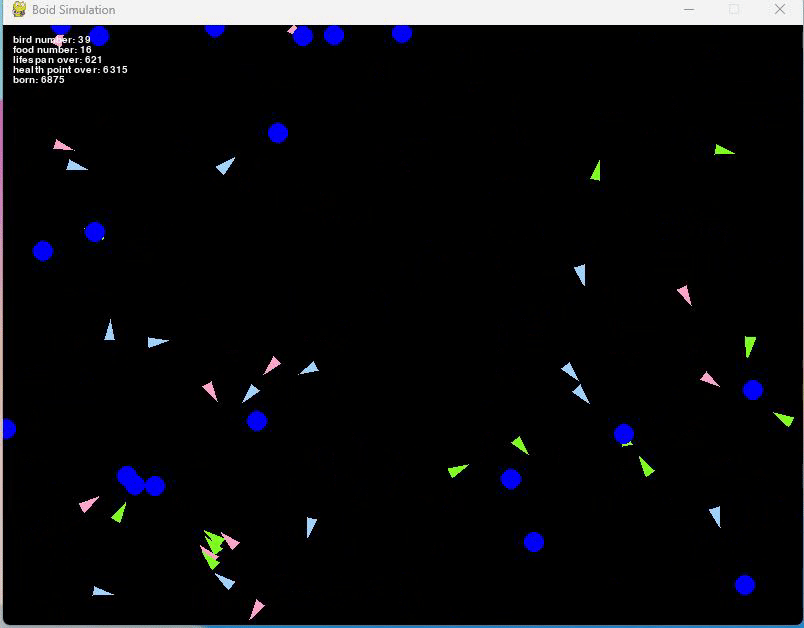
この場合、だいたい50匹前後で安定している集団となっています。
それでは、まず餌に向かうための力と餌の探索範囲を見てみましょう。
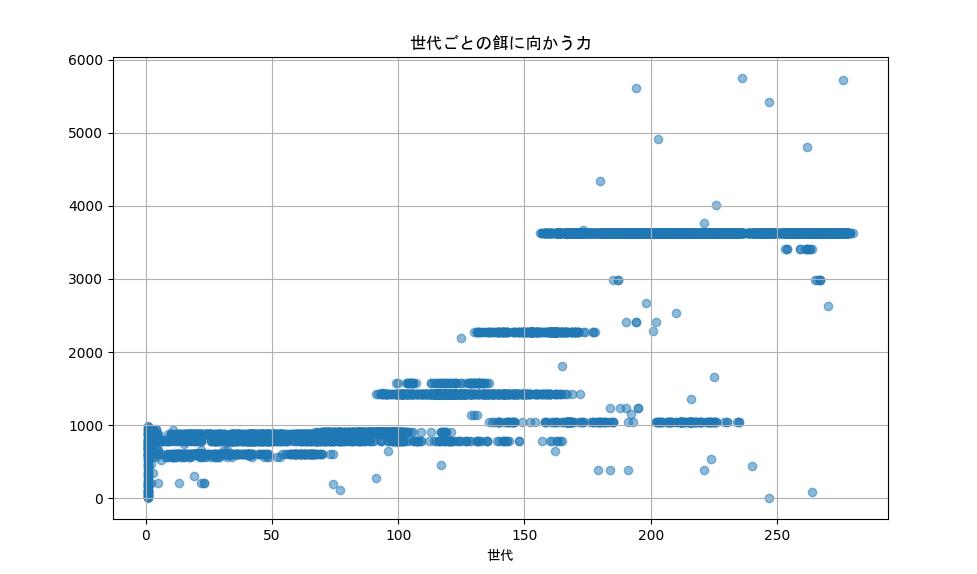
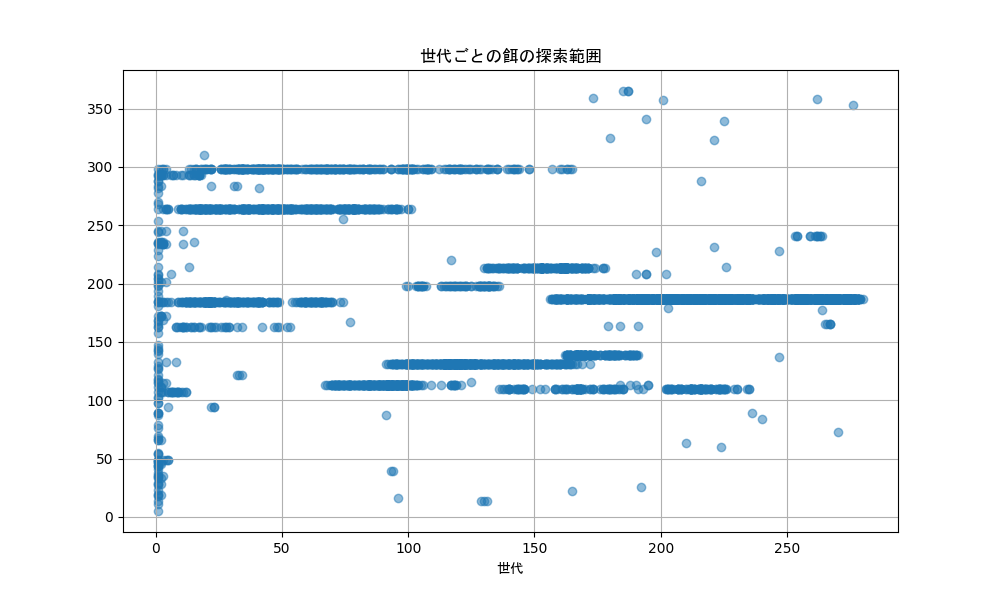
横軸は世代となります。親が子供を産むとその子供は親よりも世代が1ずつ大きくなるように設定しています。
例えば、1世代目の親同士が交配すると、子供の世代は2となります。
この散布図を見ると、体力を減らさないようにするため、餌に向かうための力はかなり強くなっていますね。
餌の探索範囲は、180前後に収束していきそうですが、割とまだランダムになっているような気がします。
実際のシミュレーションでも餌に向かう力は大きいように動いて見えました。
次に鳥の速さを分析してみます。
最初のうちは遅かったり速かったりしていますが、次第に20前後の値で固まるようになりました。
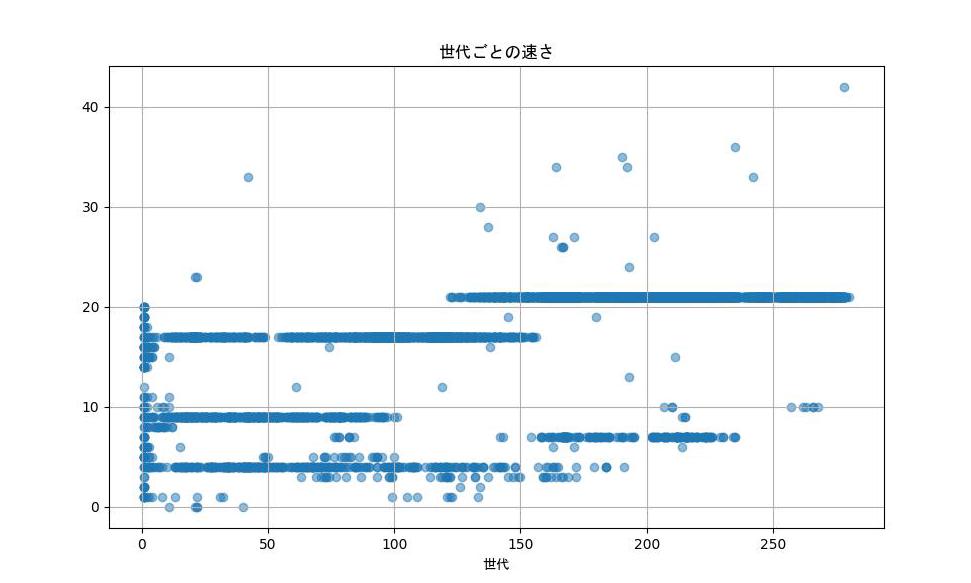
速さは体力を減らすように設定しているのでこれは意外な結果なような気がします。
体力を減らしてでも、他の鳥よりも早く餌を食べたほうが良いと判断したみたいです。
確かに実際の動物として考えると、個々の生存のため餌の取り合いが起きるので、このシミュレーションでもそれが再現されていると考えられます。
鳥自体にはルールのみ適用されている状態(つまり脳がない)なのに、実際の動物のような動きが再現されているのは面白いですね。
また繁殖するための鳥を探す範囲(鳥の交配範囲)に関しては、次第に小さくなっているのがわかりました。
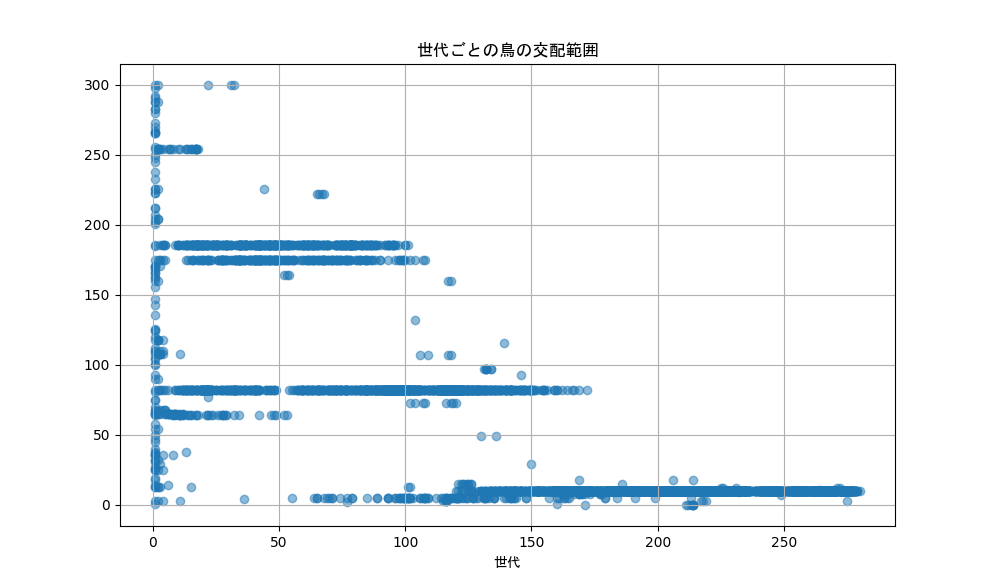
交配をすると体力が減ってしまうので当然かもしれません。
ですがそれだと個体数が減少してしまいます。
10000匹までシミュレーションできたので、繁殖はしているはずです。
もしかしたらこの環境の大きさでは交配範囲が小さくても、50匹前後の鳥たちが縦横無尽に動いていたら、鳥同士のぶつかる頻度が高く自然と繁殖できているのかもしれません。
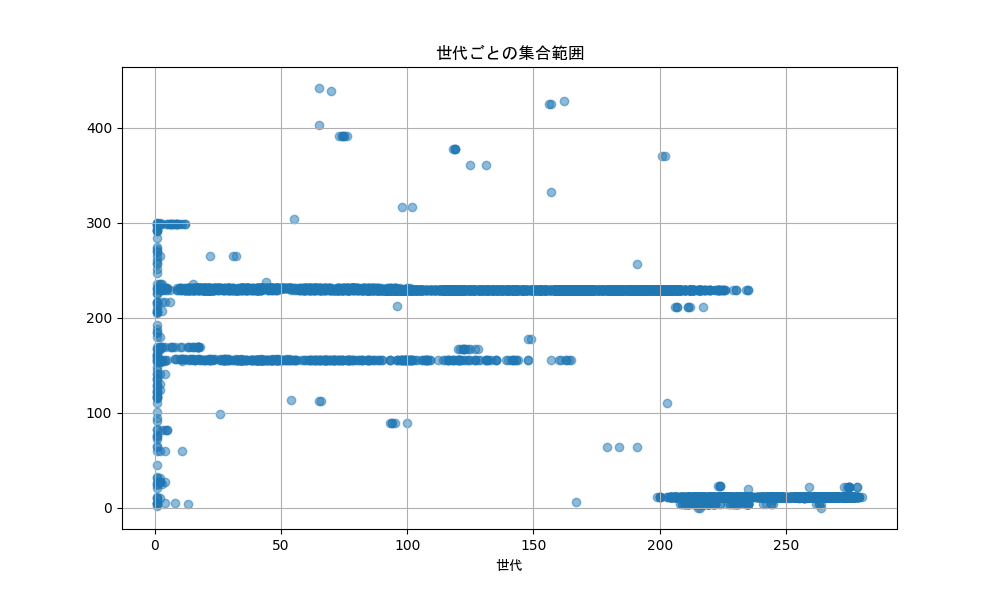
その他のパラメータも見ていくと、以下のようになります。
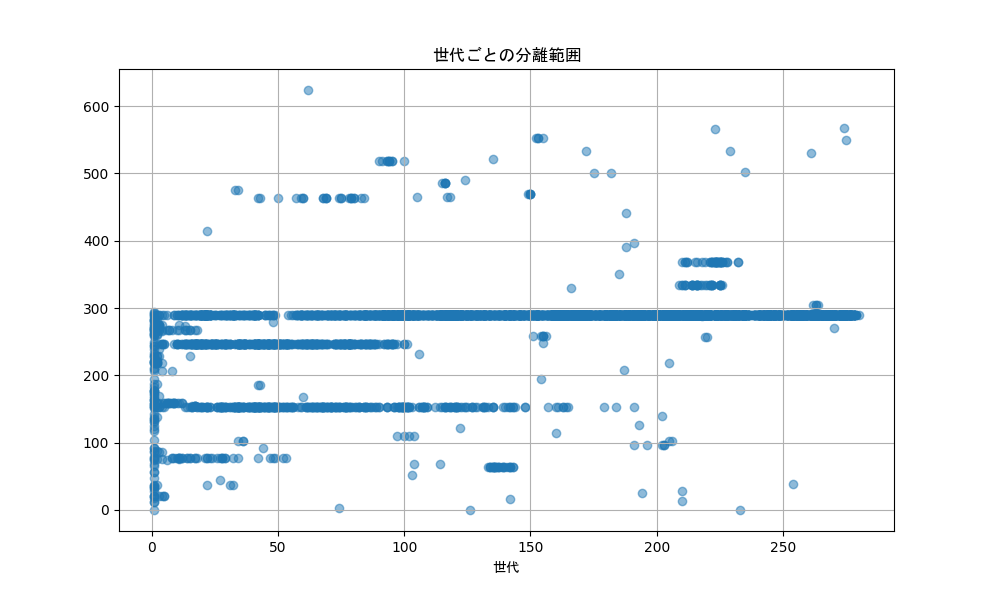
集合ルール、分離ルール、整列ルールのそれぞれで力と範囲のグラフを表にしてみました。
| 力 | 範囲 | |
|---|---|---|
| 集合 | 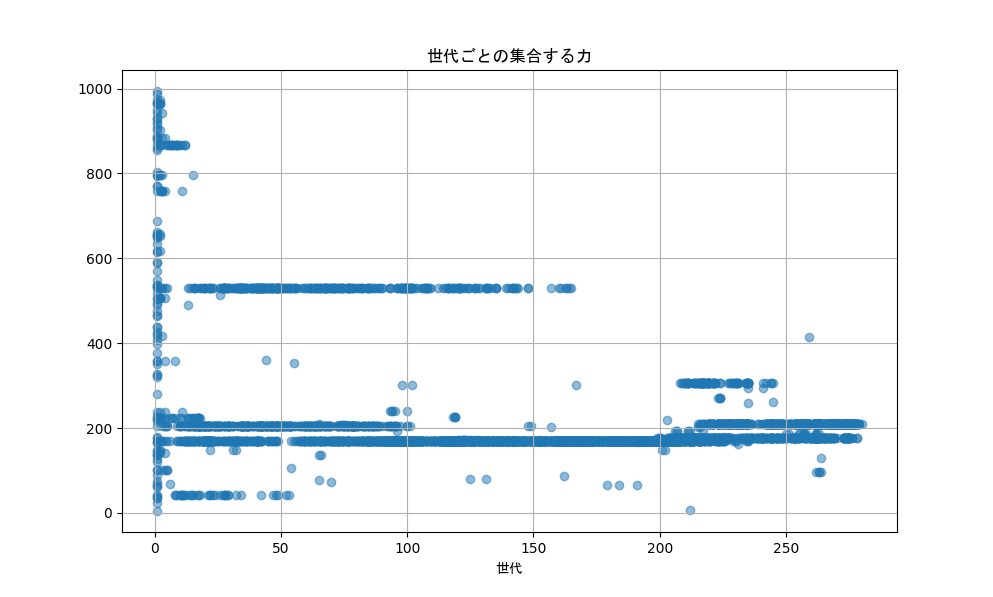 |
 |
| 分離 | 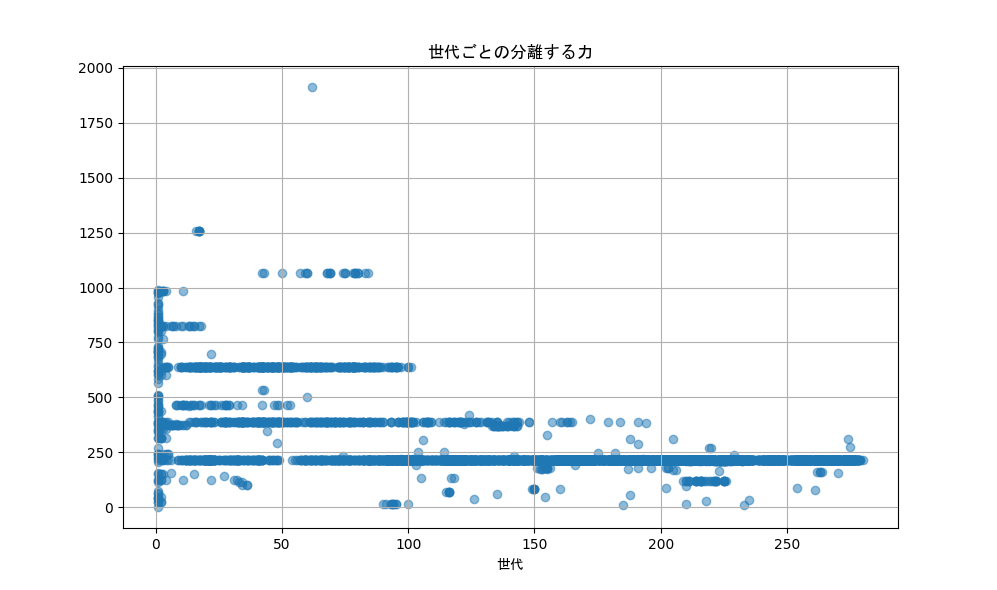 |
 |
| 整列 | 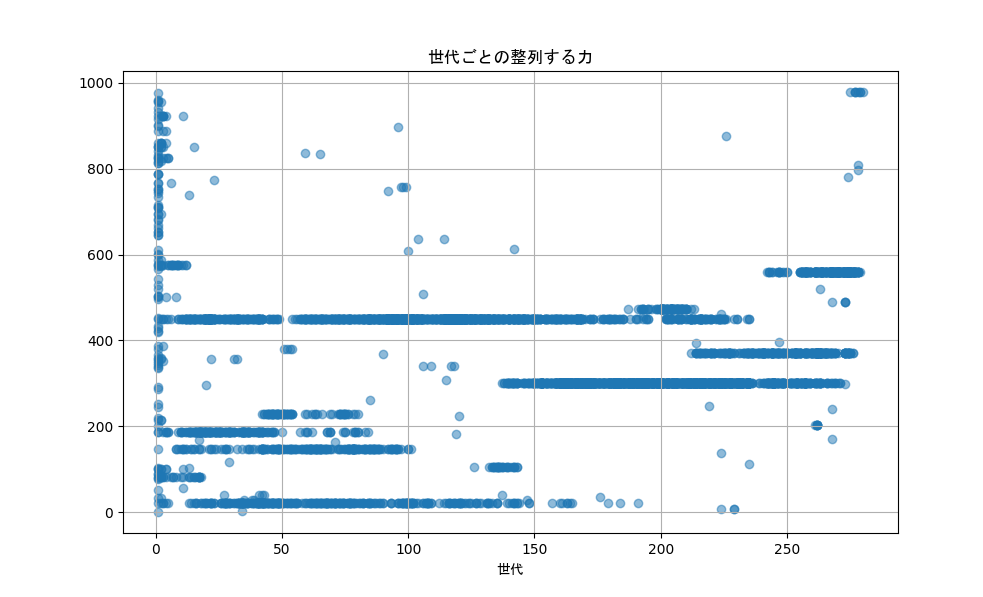 |
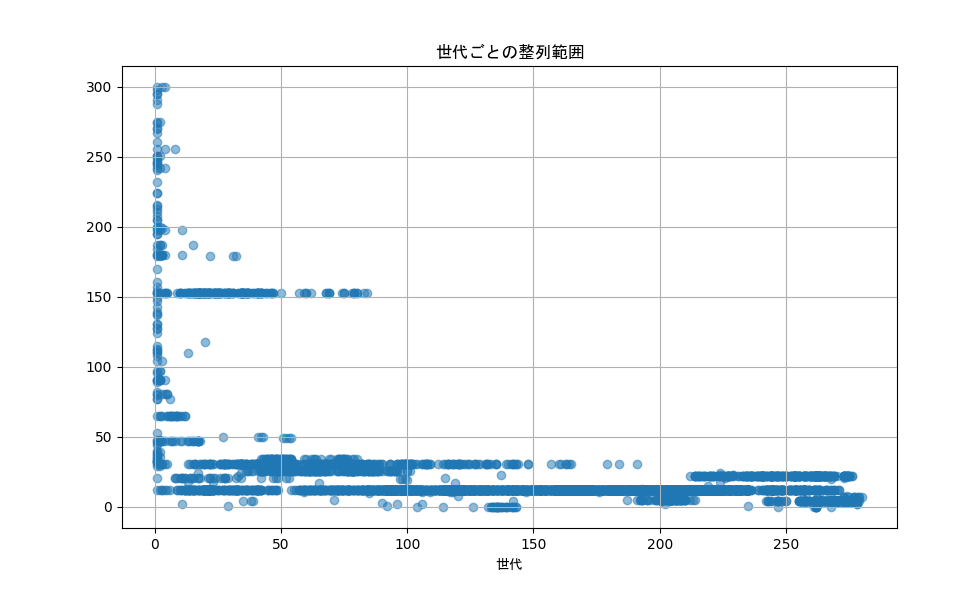 |
集合ルールや分離ルールは力が弱くなり、範囲は広くなる傾向があるみたいです。
整列ルールの場合、力は程々で、範囲は狭くなる傾向があるようです。
6つのパラメータはどれも体力には直接関係のないパラメータですが、
少なくともシミュレーションしたこの環境では群れで活動することはなく、むしろ生存する上では不必要なのでしょう。
まとめ
#今回はボイドモデルを発展させて、「体力・寿命」、「餌の探索・食事」、「繁殖」の設定を追加してシミュレーションしてみました。
繁殖をする時には簡易的な遺伝的アルゴリズムを使って、体力によるパラメータの最適化を実施しました。
約10000匹まで生成した結果、今回実験した環境では、餌を取ることを優先した個々の集団に最適化された、ということがわかりました。
今回は、鳥の初期個数を100匹、餌の初期個数を10個、新しく生まれる餌を10個、餌が生まれる確率を50%とした時のシミュレーションでした。
餌の量や出現確率、または画面サイズを調整すればまたいろんな変化が起きるかもしれません。
また今回のシミュレーションでは、産む子供に関しては1匹のみとしました。
実際の動物は大抵子供を何匹も生んでいるので、何かしらのルールを増やしつつ子を何匹も生んでみるというのも面白そうです。
実際の動物といえば、外敵の存在も重要です。
外敵を入れて外敵から逃げるような設定をすれば、また違った動きが見られそうです。
また今回の鳥の設定を応用して、外敵や餌自体も生命活動をするようになれば、自然環境そのものを再現するシミュレーションができそうです。
この場合、鳥はもちろん外敵や餌がどのような生命活動するか。3者の相互作用でどのような発展が観察できるのか。
大変興味深いです。
とはいえ、今回の生態系シミュレーションも含めボイドモデルはあくまでルールベースのモデルです。
つまり脳のない鳥がルールに従って動き回っているだけです。
動物にはもちろん考える脳がありますし、ルールそのものも人の手で設定しているので少し不自然なように個人的には感じてしまいます。
もちろん実際の動物を観察した結果の最適なルールだとは思いますが、自然界は人の手が入らずに成り立っています。
そのためルールそのものがなく鳥自身に考えさせて動かす方が、より自然な気がします。
例えば、今話題の生成AIを利用するのもひとつの手かと思います。
環境だけ設定した時に、その環境下で一匹一匹の鳥(AI)がどのように考えコミュニケーションし個々として、集団として動くのか。
考えただけでも大変面白いシミュレーションになりそうです。
まだ発展できそう(遊べそうな)シミュレーションなので、少しずつ改良を重ねていこうと思います。
ソースコード
#- GitHubにて公開しています。