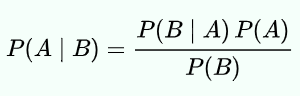転ばぬ先のベイズの定理
Back to Top前回のブログ記事でベイズ統計について簡単にご紹介しました。
今回はベイズ統計の基本中の基本である「ベイズの定理」について私の理解した範囲でご説明したいと思います。
ベイズの定理とは
#ベイズの定理は以下の式で表されます。
ここでAとBは事象であり、式として成立するためにP(B)は0ではないです。
P(A|B)は「Bを前提としてAが発生する確率(事後確率)」を示します。(条件付き確率)
P(B|A)は上記の逆で「Aを前提としてBが発生する確率」を示します。
P(A)やP(B)は、条件なしにAやBがぞれぞれ観測される確率(事前確率)を示します。
AとBは独立した事象であることが前提です。
この式は非常に面白いことを示しています。
Aを前提としてBが発生する確率は、Aが発生する確率とBが発生する確率とBを前提としてAが発生する確率から計算して求めることが出来るということです。
このP(A|B)のことを逆確率とも言います。
普通に考えると「原因」から「結果」に繋がりますが、発想を逆転させて「ある結果が発生した」状況における「原因の確率」を当てようという思想です。
例題「出荷後に障害が発生する確率」
#あるソフトウェア開発組織では「製品の出荷後に障害が発生する確率は10%である」という事が分かっていると仮定します。
だいたい10製品あればその中の1製品は出荷後に障害が発生している計算です。
さて、一人の品質保証部員が品質保証部長から調査を命じられました。
出荷後に発生している障害の内訳を調べたところ仕様に起因する障害が多そうなので、仕様レビューが正しく機能しているかを確認したいとのことです。
品質保証部員は調査を開始し、次のような結果を得たとします。
出荷後に障害が発生した製品のうち、95%は仕様レビューで不合格判断を受けたことがある。
仕様レビューで不合格判断を受けた後の仕様検討・修正・再レビューなどの対応状況についてはまだデータが集まっていませんが、上記の情報を品質保証部長に報告しました。
すると品質保証部長はカンカンになって「仕様レビューで不合格判断になったことがある製品には出荷許可を出さない!」とご立腹の様子です。
仕様レビューで不合格になったことがある = 出荷後に障害が発生
というイメージが出来上がっています。
さて、この推測は正しいのでしょうか。
確かに出荷後に障害が発生した製品のうち、95%は仕様レビューで不合格判断を受けたことがありますが、だからと言って「仕様レビューで不合格判断を受けたことがある製品は出荷後に障害が発生する」と単純に考えていいのでしょうか。
なんだかモヤモヤした気分になり、更に調査を進めました。
すると、次の事実がわかりました。
出荷後に障害が発生していない製品でも、20%は仕様レビューで不合格判断を受けたことがある。
出荷後に障害がなかった製品でも5製品のうち1製品では仕様レビューで不合格の判定を受けたことがあることがわかりました。
これらから何が言えるでしょうか。
調べてみましょう。
課題の整理
#情報を整理するために、以下のような表を作ります。
| 仕様レビュー不合格 | 仕様レビュー合格 | |
|---|---|---|
| 障害発生(10%) | 95% | 5% |
| 障害未発生(90%) | 20% | 80% |
上記の表の1列目のデータ
障害発生 & 仕様レビュー不合格 = 95%
障害未発生 & 仕様レビュー不合格 = 20%
は調査で判明した情報です。
2列目のデータ
障害発生 & 仕様レビュー合格 = 5%
障害未発生 & 仕様レビュー合格 = 80%
は1列目から残りの確率を引き算して求めてあります。
また事前の情報として
出荷後に障害が発生する確率が10%
(出荷後に障害が発生しない確率は90%)
という事が分かっています。
事後確率(逆確率)を求める
#先ほどのベイズの定理に当てはめて考えてみましょう。
今回求めたいのは「仕様レビューで不合格判断を受けたことがある製品が出荷後に障害を発生させる確率」です。
本当に高い確率なのでしょうか。
ここでは事象AとBを以下のように設定します。
事象Aを「出荷後障害発生」
事象Bを「仕様レビューで不合格判断を受けたことがある」
ベイズの定理の式から
P(A|B) : 仕様レビューで不合格判断を受けたことがある場合に出荷後障害が発生する確率
は
P(B|A) * P(A) / P(B)
となります。
上記の項目をそれぞれ求めます。
P(B|A) : 出荷後に障害が発生した製品で仕様レビューで不合格判断を受けたことがある確率 = 95%
P(A) : 出荷後に障害が発生する確率 = 10%
P(B) : 仕様レビューで不合格判断を受けたことがある確率
は先ほどの表(一列目の確率の合計)から
出荷後に障害が発生する確率(10%)× 仕様レビューで不合格判断を受けたことがある確率(95%)
と
出荷後に障害が発生しない確率(90%)× 仕様レビューで不合格判断を受けたことがある確率(20%)
を足し算して算出します。
結果は
P(B) : 仕様レビューで不合格判断を受けたことがある確率 = 27.5%
となります。
よって「仕様レビューで不合格判断を受けたことがある場合に出荷後障害が発生する確率」は
P(A|B) = 95% * 10% / 27.5% ≒ 34.5%
となりました。
事前確率である「出荷後に障害が発生する確率 = 10%」よりは高い数値ではありますが、仕様レビューで不合格判断を受けたことがあるからといって、ほとんどの製品の出荷後に障害が発生すると予測されるほどの数値ではありません。
3製品のうち1製品に障害が発生する程度の確率になっています。
品質保証部長を説得するだけの材料はそろったようです。
仕様レビューで不合格判断を受けたことがある全製品に出荷停止措置を取ってしまう前に、本当の危険率を計算できたことは成果だと思います。
ただし、仕様レビューで不合格判断を受けたことがある製品の3割以上で出荷後に障害が発生するという予測は、その製品に何らかの手立てが必要であることを示しています。
これはとても重要な情報だと思います。
確認
#では、次のようなケースではどうでしょうか。
| 仕様レビュー不合格 | 仕様レビュー合格 | |
|---|---|---|
| 障害発生(10%) | 50% | 50% |
| 障害未発生(90%) | 50% | 50% |
上記の例では
障害が発生した製品は仕様レビューで不合格判断を受けたことがある確率は50%
障害が発生しなかった製品で仕様レビューで不合格判断を受けたことがある確率も50%
です。
計算すると
P(A|B) : 仕様レビューで不合格判断を受けたことがある場合に出荷後障害が発生する確率 = 10%
となります。
つまり、事前確率から何ら変更はありません。
この例では仕様レビューで不合格だろうが合格だろうが、まったく出荷後の障害発生確率に影響の無いことがわかります。
このように情報を得ても事後確率に影響を与えない場合があるのです。
まとめ
#インターネットでベイズの定理を検索すると「ある病気の検査で陽性となった場合に病気に罹患している確率」とか「メールに”無料”というワードが含まれていた場合にメールが迷惑メールである確率」などの例題が多く見つかります。
今回は、ソフトウェア開発現場でありがちな例を取り上げて「ベイズの定理」を使って説明してみました。
参考になれば嬉しいです。
データ分析に活用して頂ければ幸いです。