相関係数だけで一喜一憂してはいけない理由
Back to Top今回は「相関行列」について解説します。
これまでデータの関係性を「平均値の差」や「分散の差」で確認してきました。
今回はデータの関係性を別な方法で確認してみましょう。
お題:「データ間の関係の強弱を見極めたい」
#あなたが品質管理者だと仮定します。
ソフトウェア開発現場から数プロジェクトの仕様書レビューの結果が持ち込まれました。
持ち込まれたデータからデータ間の関係性を見出し、次の施策につなげたいと考えています。
2つのデータに相関はあるか
#ソフトウェア開発現場から次のようなデータが示されたと仮定します。
データは次の6個の仕様書レビュー結果です。
| 欠陥密度(件/頁) | レビュー密度(人時/頁) |
|---|---|
| 0.23 | 0.30 |
| 0.15 | 0.29 |
| 0.19 | 0.22 |
| 0.19 | 0.12 |
| 0.22 | 0.64 |
| 0.20 | 0.34 |
欠陥密度は仕様書1ページ当たりのレビュー指摘件数を示し、レビュー密度は仕様書1ページ当たりのレビュー工数を示します。
あなたは直観的に
多くの工数をレビューに使った方がレビューで指摘される件数も多いのではないか?
と仮説を立てました。
では実際はどうなのか、相関係数を計算してみましょう。
相関係数とは
2群のデータの間の関係性を示す指標である。相関係数は単位を持たない。値として、正の相関が強い場合は+1に近づき、負の相関が強い場合は-1に近づき、相関が無いときは0に近い値を取る
です。
上記のデータをjamoviに入力し「相関行列」を作成して「相関係数」を計算してみましょう。
メニューの「分析」-「回帰分析」-「相関行列」を選択し、以下のように設定します。
相関行列として以下の表が出力されました。
相関の強弱の判断は以下の閾値で考えます。
(文献によって区分値が多少異なる場合がありますが、ここではおおよそで考えます)
-1 ~ -0.7: 強い負の相関
-0.7 ~ -0.5: 負の相関
-0.5 ~ 0.5: ほぼ相関なし
0.5 ~ 0.7: 正の相関
0.7 ~ 1: 強い正の相関
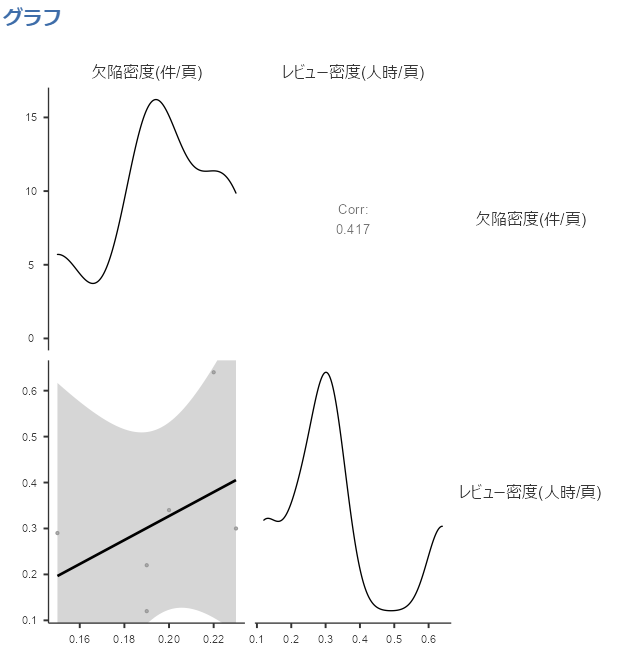
上記の判断基準からすると、今回の相関係数「0.417」は「ほぼ相関なし」に該当します。
想像していたような相関がありません。
p値から分かるように帰無仮説が棄却されているので有意ではないようです。
気を取り直してデータの分布を見てみましょう。
相関係数は外れ値の影響を受けやすいので、グラフ等でデータのばらつきを確認することが必要です。
数値ばかりに気を取られるとデータの傾向を見逃してしまう可能性があります。
グラフの灰色の部分から、データが広く分散してしまっていることがわかります。
生データでの確認
#この後、ソフトウェア開発部隊と相談して、生データを受け取りました。
先ほど比較したデータはレビュー工数とレビュー指摘件数のそれぞれを仕様書のページ数で割って算出したデータです。
もしかしたら演算の結果で本来関連のあるデータが隠れてしまった可能性があると考えました。
開発部隊からもらった生データは以下のようなものでした。
| 仕様書規模(頁) | レビュー工数(人時) | レビュー指摘件数(件) |
|---|---|---|
| 40 | 12 | 9 |
| 95 | 28 | 14 |
| 83 | 18 | 16 |
| 97 | 12 | 18 |
| 50 | 32 | 11 |
| 65 | 22 | 13 |
先ほどまでは
レビュー密度(人時/頁) = レビュー工数(人時) ÷ 仕様書規模(頁)
欠陥密度(件/頁) = レビュー指摘件数(件) ÷ 仕様書規模(頁)
を事前に計算していましたが、今度はすべて元々の数値を使用します。
jamoviにデータを設定し、それぞれの相関を計算させました。
ツールを使うと複数の要因間の関連も簡単に見ることができます。
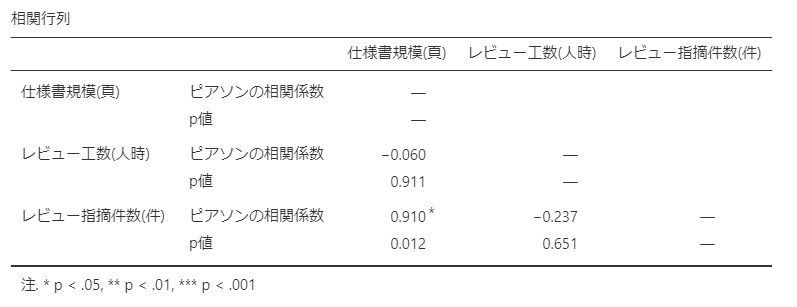
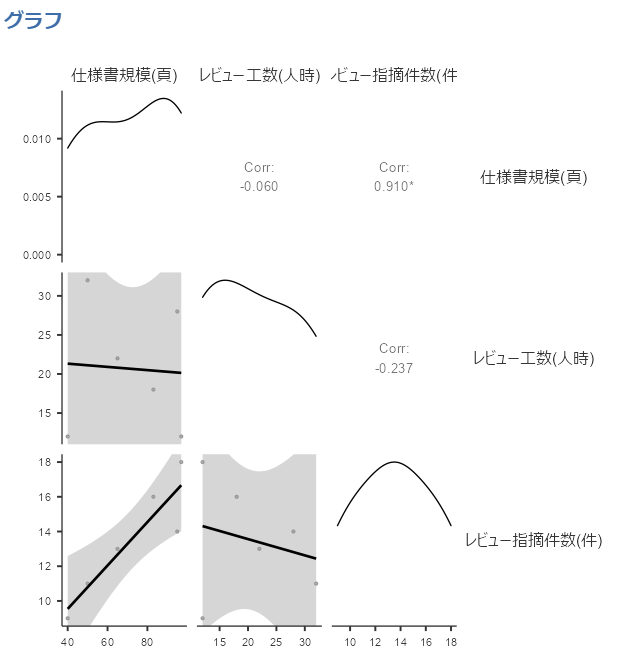
相関行列として以下の表が出力されました。
今度は「仕様書規模とレビュー指摘件数」の間に相関がありそうです。
p値も有意を示しています。
グラフも確認しましょう。
上図からも「仕様書規模とレビュー指摘件数」にかなり強い相関がありそうなことが見て取れます。
しかし、他の
仕様書規模とレビュー工数
レビュー工数とレビュー指摘件数
の間には相関が見られません。どちらかというと負の相関になっています。
レビューは適切に管理・運営されているか
#「仕様書規模とレビュー工数」の間に相関が無かったのは、ソフトウェア開発部隊側でレビューに工数を割り当てる時の采配による影響かもしれません。
しかし、「レビュー工数とレビュー指摘件数」に相関が無いのはなぜでしょう?
工数を多く使った分だけ効果(欠陥除去)があっても良いと考えていたので不思議です。
これはあくまで想像ですが、レビュー自体が
レビューという名の会議だった
レビューアに新人が多くて指摘が出なかった
仕様書の説明会だった
など、レビューが「欠陥を摘出する活動」として機能していないレビューも多く存在したのではないかと想像できます。
要因の設定ミスによって「本来は相関があるのに相関が無いように見える」ことがあります。
また、データを手当たり次第に収集して相関を取ってしまうと「本来は関係がないのに相関があるように見える」ケースも出てきてしまいます。
まとめ
#相関行列は非常に便利で、データ間の関係を読み解くのに使われます。
要因数が2つぐらいだったら相関を視覚的・感覚的に見ることも可能ですが、要因数が多い場合は相関行列を使った方が理解は早いでしょう。
ただ、今回の例のように要因の設定を誤ると、間違った解釈をしてしまうこともあります。
データを味方につけて、慎重に分析・改善につなげていくことが大事だと考えています。
よろしければ他のブログ記事も参照ください。
データ分析に活用して頂ければ幸いです。