机器人开发者的强化学习入门
Back to Top为了覆盖更广泛的受众,这篇文章已从日语翻译而来。
您可以在这里找到原始版本。
引言
#本文将通过处理控制领域中熟知的倒立摆问题,讲解强化学习的基本理论和实践方法。通常面向强化学习初学者的文章多以探索迷宫的程序或老虎机作为例子来说明,但对于对机器人或机器控制感兴趣,或者想将其应用到这些领域的人来说,倒立摆这样的问题可能更容易理解。
CartPole任务概述
#本文将采用由 Gymnasium[1] 提供的 CartPole任务。
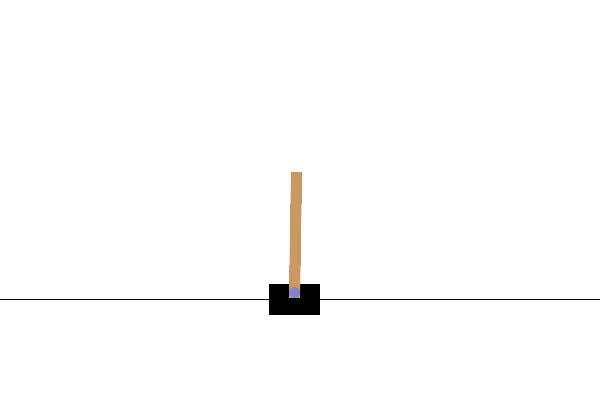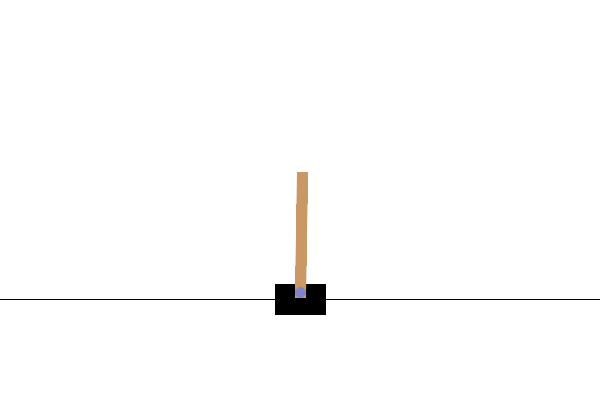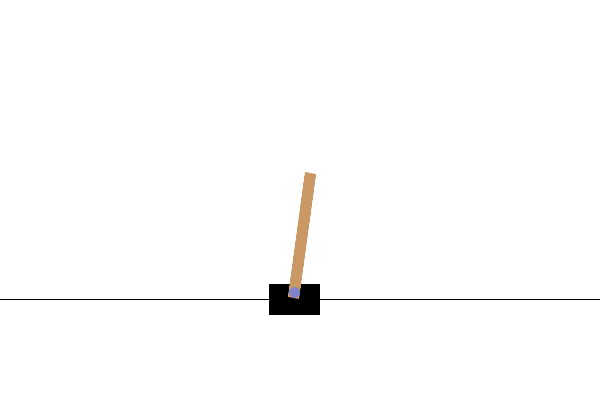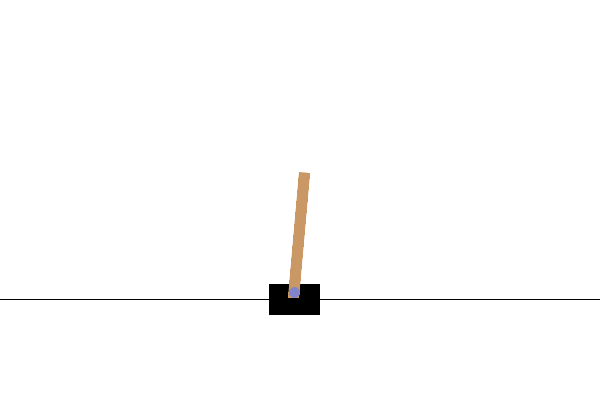
在此任务中,通过在小车左右施加力,目标是保持杆子的平衡。当杆子倾斜超过一定角度,或小车超出屏幕两侧时,即判定为失败并结束。在强化学习中,从任务开始到结束的整个过程被称为回合。上方的 GIF 图像显示了在学习尚未完善的状态下,回合迅速结束并不断重试的情形。
状态与动作
#我们称从系统中观察到的信息为状态。
下表展示了该系统中状态的各个要素以及回合的结束条件。
| 状态要素 | 回合结束条件 | |
|---|---|---|
| 0 | 小车位置 | 当 或 时结束 |
| 1 | 小车速度 | - |
| 2 | 杆角 | 当 时结束 |
| 3 | 杆角速度 | - |
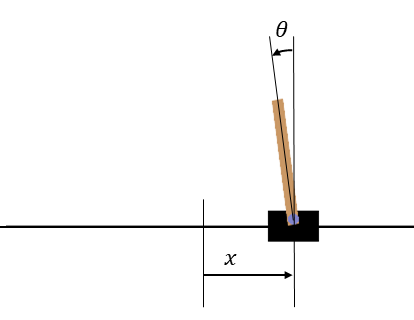 CartPole的坐标轴。x 轴的原点在屏幕中央,θ 以屏幕上方为 0°。
CartPole的坐标轴。x 轴的原点在屏幕中央,θ 以屏幕上方为 0°。
对系统的输入在强化学习中称为动作。在 CartPole 任务中,可以选择“向左推小车”或者“向右推小车”的动作。由于施加的力是固定的,因此不像 PID 控制那样可以进行细致的输出调节。需要注意的是,如果使用与本文不同的方法,也可以处理可变的动作。
与迷宫或老虎机不同,在控制问题中必须注意控制周期。CartPole 任务默认设置的控制周期为 0.02秒,在每个周期内都会重复获取状态和选择动作。
学习机制
#从这里开始,我们考虑利用强化学习来解决上述 CartPole 任务。
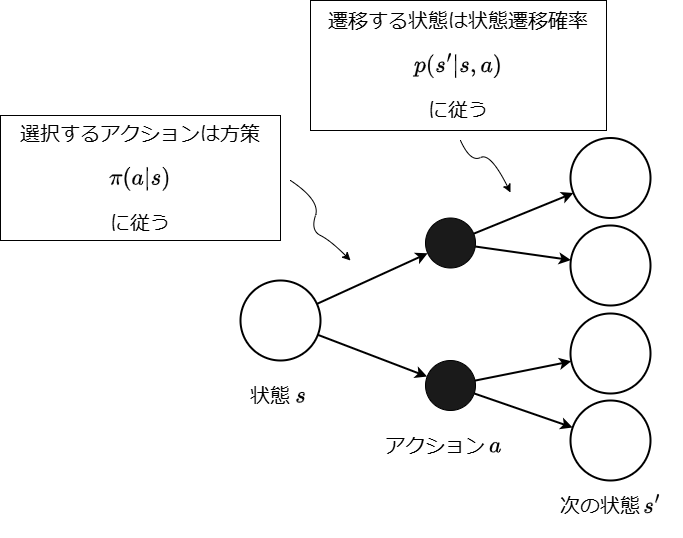
在强化学习中,决定动作的主体称为智能体(Agent),而被智能体操作的对象称为环境。
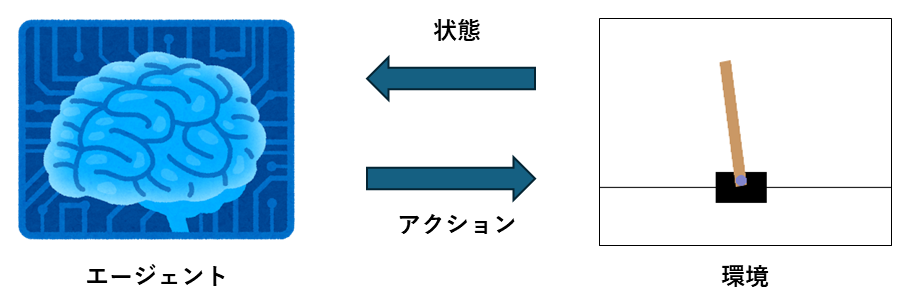
强化学习的目标是使系统能够基于获得的状态选择最优的动作。
将状态映射到动作的函数称为策略,记作 。
奖励与收益
#在这里将介绍强化学习中重要的概念——奖励和收益。
奖励是指智能体在每一步中从环境中获得的数值,表示当时动作的“好坏”。用于计算奖励的函数称为奖励函数,通常需要开发者根据任务设计奖励函数。在 Gymnasium 所提供的任务中,奖励函数已预先设定,因此这里直接使用。对于 CartPole 任务,只要杆子保持竖直,每一步即可获得奖励1。
收益是指智能体获得的奖励从当前步骤延伸到未来所有步的总和。若第 步获得的奖励为 ,则收益可表示为:
这里 被称为折扣率,其取值在0到1之间。折扣率有防止收益发散的作用。[2]
奖励与收益的关系可类比为年收入与终身收入的关系。每次动作获得的是奖励(年收入),但不能只看眼前的金钱。智能体会选择使长期指标收益(终身收入)更高的动作。
顺便提一句,由于折扣率的影响,近期开出的奖励价值会被高估,而远期奖励的价值则被低估。
利用价值函数选择动作
#在强化学习中,学习的目标是能够选择使收益最大化的动作。但由于计算具体收益需要未来的奖励,因此在选择动作时采用了收益的期望值。用于计算这种收益期望值的函数被称为价值函数。
状态价值函数与动作价值函数
#价值函数中,有只以状态为参数的状态价值函数,以及以状态和动作两个参数为基础的动作价值函数。
状态价值函数 可表示为:
同时,动作价值函数 则利用所选动作 表示为:
其中, 表示对收益 取期望值。
在这里,为了探讨状态价值函数的具体形式,引入备份示意图。
备份示意图使用表示状态的白色圆圈和表示动作的黑色圆圈来表达概率性状态转移。
在强化学习中,动作的选择以及动作执行后状态的变化都被视为具有概率性的过程。[3]
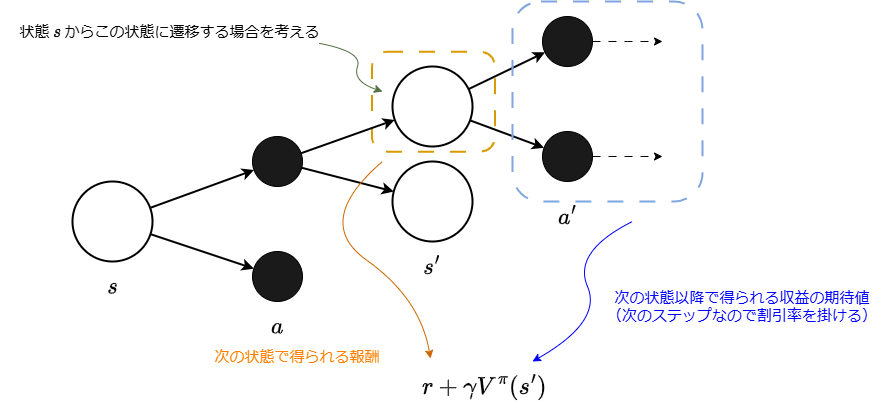
下图展示了在状态 下选择动作 ,并转移到下一个状态 的备份示意图。
为了计算期望值,需要计算“结果值”ד该结果发生的概率”的乘积并求和。这里所说的“结果值”是指转移到某个状态 时所获得的收益。此外,由于状态从 转移到下一个状态 时存在策略与状态转移两种概率因素,因此需要进行两次求和。
先考虑“结果值”。如下图所示,从状态 选择动作 转移到下一个状态 时获得的收益可表示为:
这表示将状态 所获得的奖励与其后的收益分别表达出来。
得到了“结果值”后,接下来考虑其发生概率来计算期望值。
在选择了状态 与动作 后,可通过状态转移概率 表示转移到可能状态 时获得的收益期望值,如下所示:
这表示选择某个动作 所对应的收益期望值,因此考虑状态 下所有可能选择的动作,就可以表示状态 下的收益期望值。
采用表示在状态 下选择动作 的概率的策略 ,可得以下公式:
该公式被称为贝尔曼方程,是强化学习的重要概念之一。
总结来说,贝尔曼方程由以下要素构成:
- :概率策略
- :状态转移概率
- :从状态 转移到 时的奖励
- :下一步及之后收益期望值 × 折扣率
同样地,按照相同思路计算动作价值函数 ,得:
针对 CartPole 进行简化
#上述贝尔曼方程假设策略与状态转移均为概率性的建模。但在 CartPole 中,执行动作后的状态是唯一确定的(称为确定性的),因此该公式可以简化。
简化后的备份图及动作价值函数如下所示。
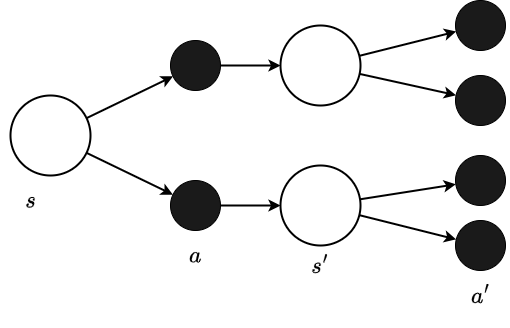
与之前的备份图不同,这里动作后的状态只有一个。
利用动作价值函数选择动作
#引入价值函数的目的在于选择能够获得更高收益的动作。由于动作价值函数的输出代表“在某个状态 下选择动作 所获得的收益期望值”,因此可以判断应选择哪个动作。
通过比较状态价值来选择动作的方法只是强化学习方法中的一种例子。
这种方法称为基于价值的方法.
部分可视化价值函数
#虽然已经介绍了价值函数,但为了更深入理解,我们来考虑该函数的图形。但不是为了完全掌握整体,而是考虑某个状态下的收益期望值。
这里考虑以下两个状态:
- 杆子稳定竖直的状态
- 杆子即将倒下的状态
首先考虑杆子稳定直立的状态。也就是说,这种状态下在未来各步还能持续获得奖励。重述收益公式:
在该公式中,奖励被累加到无穷步,但这种收益的前提是回合没有结束,如果杆子在此之前倒下,则收益为到当步为止的奖励总和。当获得至 步的奖励时,收益如下图所示。
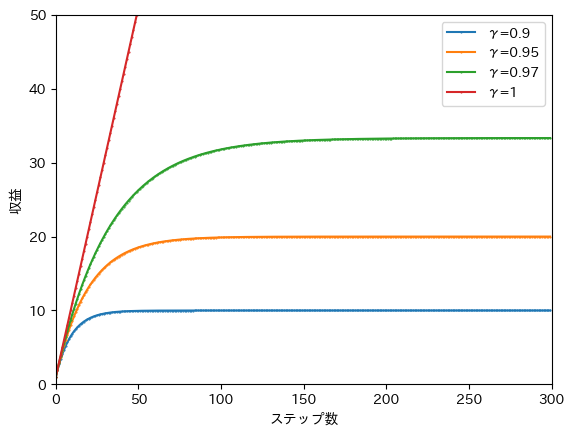
由于折扣率的影响,收益会收敛,并且收敛的值取决于折扣率。
例如,从采用折扣率 的橙色曲线可以看出,当回合超过 100 步时,收益约为20。
接下来我们查看在失衡导致回合结束前的状态价值。如下图所示,考虑一种状态 ,其中杆角略微处于回合结束条件(的线以内),但正向越过该线有较大角速度。从此状态转移到下一状态。注意,虽然对结果无影响,但计算时假设两种动作各以50%的概率选取。
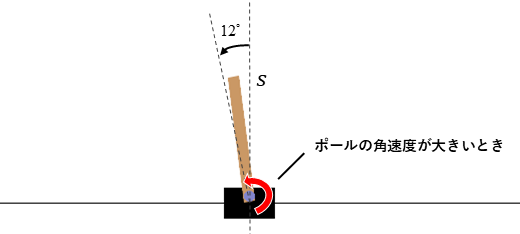
此时考虑状态价值如下:
其中 表示转移到下一状态 时所获得的奖励。这是 CartPole 的设定,即使转移到的状态 满足回合结束条件,也能获得奖励1。而接下来无法获得奖励的收益期望值 为 0。因为不论选择哪个动作,状态 都符合回合结束条件,之后不再发生状态转移。因此,上图中状态 的状态价值为 1。
那么,考虑主题——价值函数的形式。需要注意的是,状态价值函数的参数状态 是一个四维向量,直观可视化较为困难。这里为了传达大致的概念,我们仅将杆角作为变量,而将小车位置、小车速度以及杆角速度固定为0时,绘制收益的图像。
当折扣率 时,状态价值函数的图形如下面所示。[4]
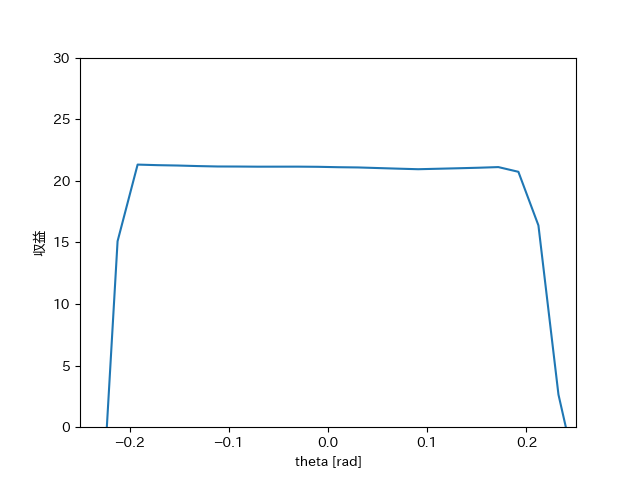
首先在 附近,由于杆子稳定直立,所以收益约为20。同时,在回合结束条件附近(即 (约 ))时,价值会下降。
用神经网络近似动作价值函数
#在将动作价值函数应用于 CartPole 任务时需要进一步的技巧。
前面公式中状态记为 ,而 CartPole 的状态由如下四维向量构成。(为加以区分,这里用加粗的 表示。)
包含此状态的动作价值函数可以描述为:
这样当状态跨越多个维度时,手工定义动作价值函数十分困难。因此,用神经网络**近似动作价值函数 **的想法便出现了,这正是著名的 DQN(Deep Q-Network)[5] 的理念。
所谓 Q 网络,即用神经网络替代动作价值函数 。
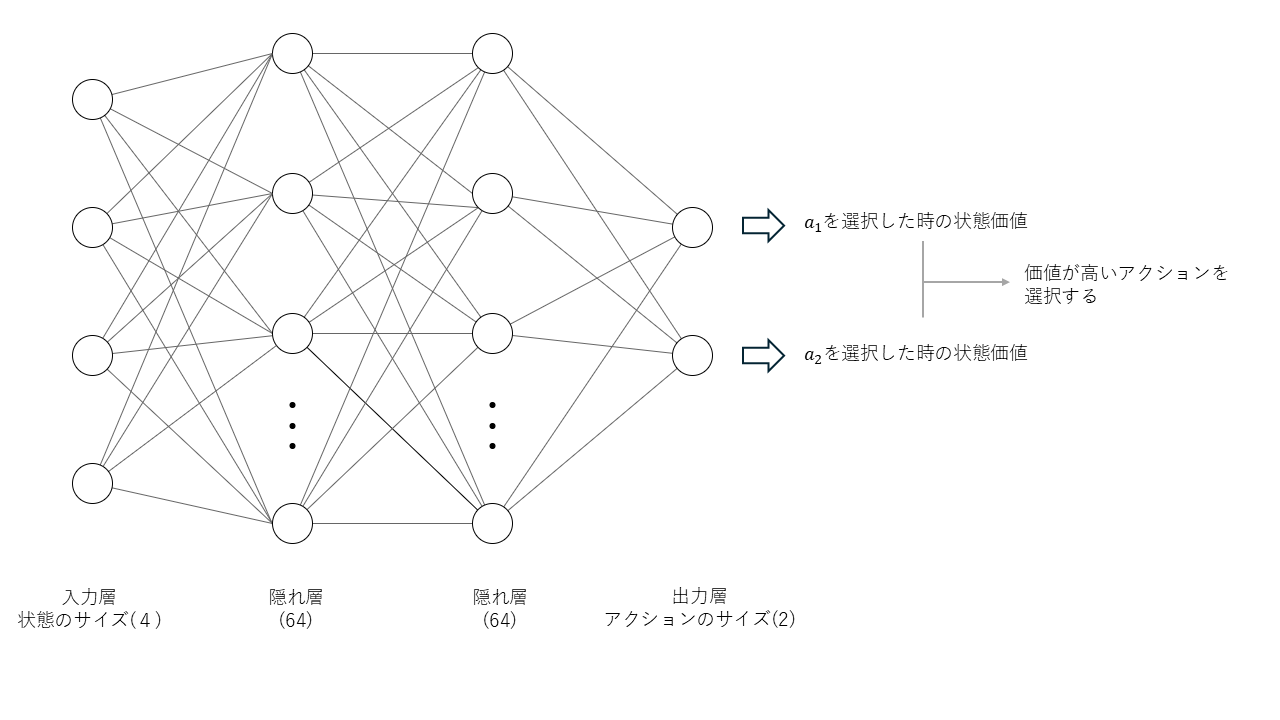
DNN 架构
#这里使用具有两个隐藏层的 DNN[6]。输入层有 4 个单元用于输入状态,输出层的单元数与动作数量一致。输出层中每个单元的值表示对应动作的动作价值,从中选择动作价值最高的动作执行。
DNN 的训练
#通常神经网络的训练需要数据集。但在强化学习中,并非预先准备好数据集,而是利用智能体与环境之间交互产生的数据。
对于 Q 网络,同一般神经网络一样,仍然是定义损失函数并最小化损失的框架。损失函数定义为使目标值 (称为 Target)与当前值 之间的差最小化。
其中 被称为 目标,其定义如下:
- :采取动作 时获得的奖励
- :对动作中价值最大的那个动作的动作价值
学习流程
#总结一下前面所介绍的内容。
- 重复以下内容直至学习完成:
- 智能体从环境中获取初始状态。
- 重复以下过程直至学习结束:
- 智能体利用动作价值函数从状态中选择动作。
- 智能体执行动作后,环境的状态发生变化。
- 环境根据动作内容和状态转移情况返回奖励给智能体。
- 智能体利用保存的状态、动作和奖励更新动作价值函数(Q 网络)。
使用 DQN 算法进行学习实践
#接下来我们处理 CartPole 任务。另外,本文中使用的源代码已上传至以下仓库。
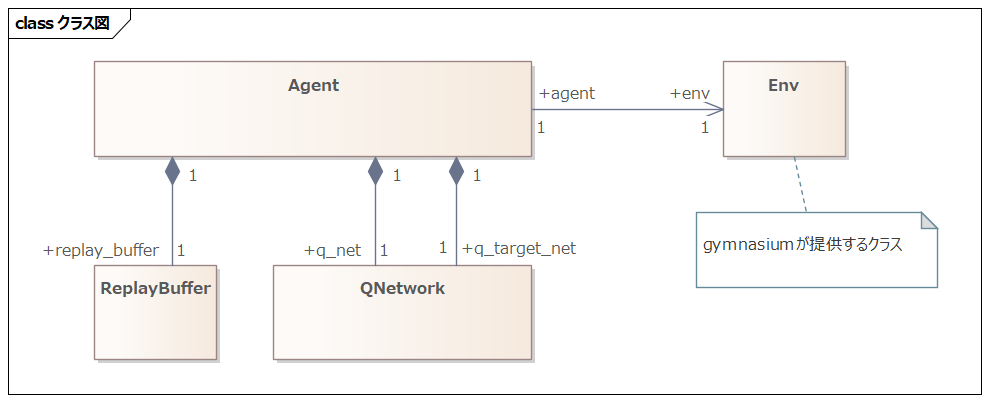
类结构
#正如开头所述,CartPole 是包含于 Gymnasium 这个强化学习库中的任务。由于 Env(环境)类使用 Gymnasium 提供的,因此其他类需要自行实现。
ReplayBuffer 类是用于保存状态、动作与奖励历史的类。智能体会将状态等信息存储到此类中,在更新 Q 网络时提取数据。
学习的执行与结果
#执行 main.py 即可开始学习。
from datetime import datetime
import gymnasium as gym
from agent import DQNAgent
# episode: 回合数
episodes = 3000
# sync_interval: 同步 Q-network 的间隔
sync_interval = 20
env = gym.make("CartPole-v1", render_mode="human")
# env = gym.make("CartPole-v1")
agent = DQNAgent("cpu")
reward_history = []
for episode in range(episodes):
observation, info = env.reset()
done = False
total_reward = 0.0
print("episode: ", episode)
while not done:
# 传入初始状态并获取动作
action = agent.get_action(observation)
# 推进环境到下一步
next_obs, reward, terminated, truncated, info = env.step(action)
agent.update(observation, action, reward, next_obs, terminated)
observation = next_obs
total_reward += reward
env.render()
if truncated or terminated:
print(" done : total_reward: ", total_reward)
print(" terminated: ", terminated, "truncated: ", truncated)
done = True
if episode % sync_interval == 0:
agent.sync_qnet()
postfix = datetime.now().strftime("%Y%m%d_%H%M%S")
agent.save_model(postfix)
在学习初期(~100 回合),很快就会失去平衡而回合结束。

然而,随着进一步的学习,系统逐渐能保持平衡。
检查学习是否顺利进行的一种方法是观察横轴为回合数、纵轴为累计奖励的图表。随着学习的深入,累计奖励应当增多,因此期望看到一条上升的曲线。以下展示的是 3000 回合学习时的示例图。
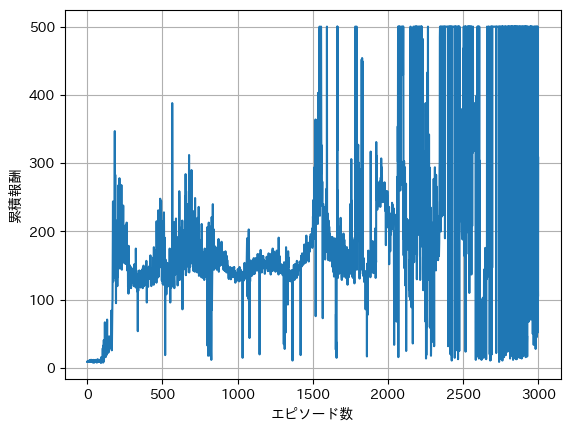
从图中可以看出,只有在超过1500回合时,才会达到500步,但也有一些回合在进行过程中仅坚持了几十步便失败。当前方法由于使用 -greedy 算法,因此以一定概率选择非最优动作,即使学习进展顺利也可能早期失败。
为消除这种影响,进行了 20 次 3000 回合的学习,并取平均值,如下图所示。
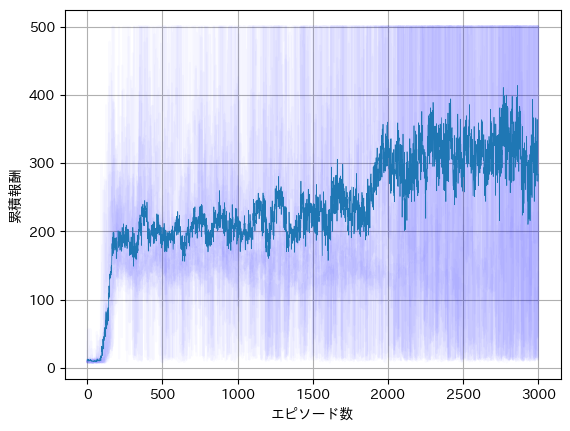
实线表示20个回合的平均,个别曲线则以淡色展示。与前图相比,可以看出整体呈上升趋势。
保存与利用已学模型
#到目前为止已经说明了智能体如何学习 CartPole 任务,接下来也介绍保存或再利用学到结果的方法。
在本方法中,神经网络通过学习获得了能很好近似动作价值函数 的参数。因此只要保存这些参数,就可以实现学到结果的再利用。
不同的库保存训练后参数的方法各不相同,但在本次使用的 pytorch 中,可以通过如下处理将参数保存到文件中。
def save_model(self, postfix: str):
filename = f"q_net_{postfix}.pth"
torch.save(self.qnet, filename)
此外,在训练时,为了经历各种状态,智能体以一定概率选择随机动作。
在实际应用时,将修改为始终选择具有较高动作价值的动作。
before(探索あり)
def get_action(self, state: np.ndarray) -> int:
if np.random.rand() < self.epsilon:
# 随机选择动作(探索)
return np.random.choice(self.action_size)
else:
# 选择 Q 值最大的动作(利用)
state_as_tensor = torch.tensor(state[np.newaxis, :],dtype=torch.float32)
qs = self.qnet(state_as_tensor)
return qs.argmax().item()
after(探索なし)
def get_action(self, state: np.ndarray) -> int:
# 选择 Q 值最大的动作(利用)
state_as_tensor = torch.tensor(state[np.newaxis, :],dtype=torch.float32)
qs = self.qnet(state_as_tensor)
return qs.argmax().item()
不进行探索而始终选择最优动作的智能体能够连续存活500步。

结束语
#本文以 CartPole 任务为题材,介绍了基本的强化学习内容。
在此次介绍的方法中,对于将状态转换为动作价值的部分使用了神经网络,但是也可以用于策略函数,或者结合多个网络使用。另外,近年来出现了不仅仅是这种简单网络,而是使用 LLM 或 VLM 的方法。能根据要实现的任务组合各种技术,也是强化学习有趣之处。
参考资料
#Reinforcement Learning:An Introduction
Gymnasium 是一个为支持强化学习算法开发和研究而提供仿真环境的 Python 库。 ↩︎
如果如本例中奖励是固定值,则收益可视为等比数列的和,其收敛性已被证明。 ↩︎
概率性状态转移的例子,例如汽车打滑。当选择“前进”这个动作时,汽车位置的变化或者由于打滑而未变化,都可以看作是概率现象。 ↩︎
这是使用后文所述的 DNN 输出制作的图。 ↩︎
Deep Q-Network. https://arxiv.org/abs/1312.5602 ↩︎
在 DQN 中网络结构并非固定为特定形态。本文中由于状态以四维向量给出,因此使用全连接型 DNN。原论文中为提取游戏画面的特征采用了 CNN。 ↩︎