ロボット開発者のための強化学習入門
Back to Topはじめに
#本記事では、制御の分野ではおなじみの倒立振子の問題に取り組みながら、強化学習の基本的な理論とその実践方法について解説します。
強化学習の初心者向けの記事では、迷路を探索するプログラムやスロットマシンを例として挙げながら説明するものが多い印象がありますが、ロボットや機械の制御に関心がある、またはそれらの分野への応用を考えている人にとっては倒立振子のような問題のほうが分かりやすいのではないかと思います。
CartPoleタスクの概要
#本記事ではGymnasium[1]が提供するCartPoleタスクを取り上げます。
このタスクでは、カートに左右から力を加えることで、ポールのバランスを取り続けることを目指します。ポールが一定の角度以上に傾くと、またはカートが画面の両端よりも外側に出ると失敗となり、その時点で終了します。タスクを開始してから終了するまでを、強化学習ではエピソードという単位で表します。上のGIF画像は学習が不完全な状態であり、短時間でエピソードが終了し、リトライを繰り返している様子です。
状態とアクション
#システムから観測できる情報を状態と呼びます。
下記の表はこのシステムにおける状態の要素とエピソードの終了条件です。
| 状態の要素 | エピソードの終了条件 | |
|---|---|---|
| 0 | カート位置 | で終了 |
| 1 | カート速度 | - |
| 2 | ポール角度 | で終了 |
| 3 | ポール角速度 | - |
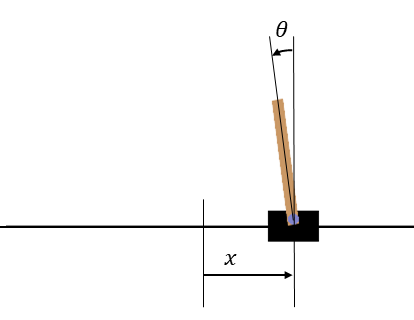 CartPoleの座標軸。xの原点は画面中央、θは画面上方向が0°となる。
CartPoleの座標軸。xの原点は画面中央、θは画面上方向が0°となる。
システムへの入力を強化学習ではアクションと呼びます。CartPoleタスクでは、アクションとして「左へカートを押す」と「右へカートを押す」のいずれかが選択できます。押す力は一定なので、PID制御のように出力を細かく調整できません。なお、この記事で扱うものとは別の手法を用いれば、可変のアクションを扱うことも可能です。
迷路やスロットマシンと異なり、制御では制御周期を気にしなければなりません。CartPoleタスクではデフォルトの制御周期として0.02秒が設定されており、この周期ごとに状態の取得とアクションの選択を繰り返します。
学習のしくみ
#ここからは上記のCartPoleタスクを強化学習を使って解くことを考えます。
強化学習ではアクションを決定する主体をエージェント、エージェントが操作する対象を環境と呼びます。
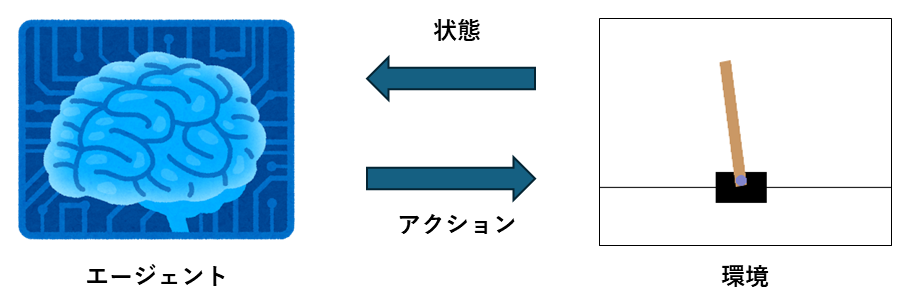
強化学習のゴールは、得られた状態に基づいて最適なアクションを選択できるようになることです。
状態をアクションへとマッピングする関数を方策といい、で表します。
報酬と収益
#ここで強化学習において重要な概念である報酬と収益について説明します。
報酬とはエージェントがステップ毎に環境から受け取る数値であり、その時点での行動がどれだけ「良かった」かを表す指標です。報酬を計算する関数を報酬関数といい、通常は開発者がタスクに合わせた報酬関数をデザインする必要があります。Gymnasiumが提供するタスクでは報酬関数はあらかじめ設定されているため、今回はそれを使用します。CartPoleタスクではポールが立っている間はステップ毎に1の報酬が得られます。
収益はエージェントが得る報酬を将来のステップまで含めて合計した値です。番目のステップで得られる報酬をとするとき、収益は次のように表します。
ここでは割引率といい、0から1の値をとります。割引率には収益が発散することを防ぐ役割があります。[2]
報酬と収益の関係は年収と生涯年収の関係に例えられます。アクションのたびに得られるのは報酬(年収)ですが、目先の金に目が眩んではいけません。エージェントはより長期的な指標である収益(生涯年収)が高くなるような行動を選択します。
ちなみに収益には割引率の影響により、近いうちに得られる報酬の価値を高く、先にならないと得られない報酬の価値は低く見積もるような補正がかかります。
価値関数を用いてアクションを選択する
#強化学習では収益を最大化するようなアクションを選択できるように学習します。しかし具体的に収益を計算するためには未来の報酬が必要です。そのため、アクションの選択には収益の期待値を使用します。この収益の期待値を計算するための関数を価値関数と呼びます。
状態価値関数と行動価値関数
#価値関数には、引数に状態のみをとる状態価値関数と、状態と行動の2つの引数をとる行動価値関数があります。
状態価値関数は、収益、現在の状態を使って次のように表されます。
また、行動価値関数は、選択したアクションを使って次のように表されます。
ここでは収益の期待値をとることを表しています。
ここで、この状態価値関数の具体的な形を考えるために、バックアップ線図を導入します。
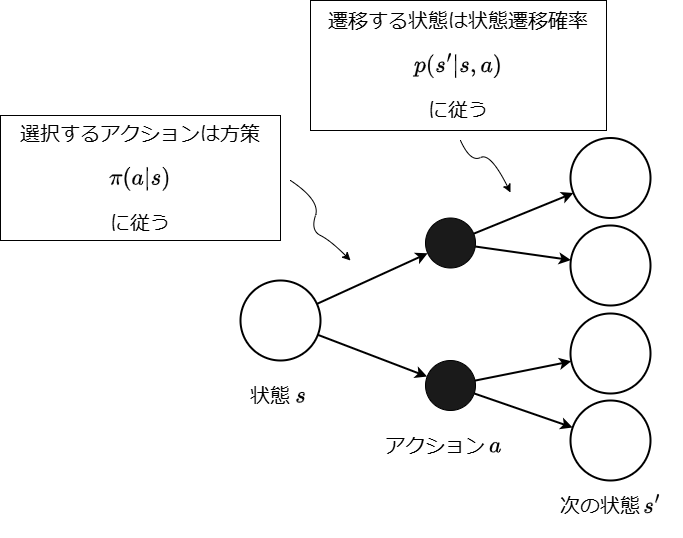
バックアップ線図は状態を表す白い丸とアクションを表す黒い丸を用いて、確率的な状態遷移を表現します。
強化学習では、アクションの選択も、アクションの実行による状態の変化も、確率的なものとして扱います。[3]
下図は、状態でアクションを選択し、次の状態に遷移することを表したバックアップ線図です。
期待値を計算するためには、「結果の値」×「その発生確率」を計算し、総和をとります。ここでいう「結果の値」とは、ある状態に遷移したときの収益です。また、状態が次の状態へ遷移する間には、確率的な要素が方策と状態遷移の2つあるため、総和を2回計算する必要があります。
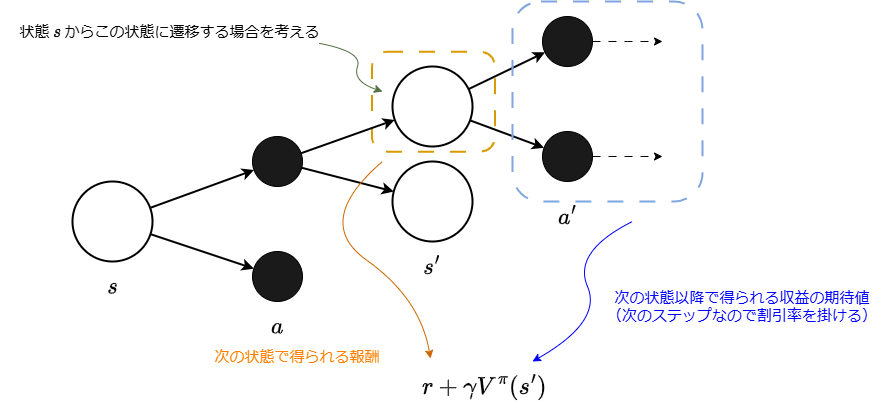
まず「結果の値」を考えます。下図のように、ある状態からアクションを選択し、次の状態に遷移した場合の収益は次のように表現できます。
これは状態で得られる報酬と、それ以降の収益を分けて書いた表現になります。
「結果の値」が求まったので、次にその発生確率を考慮しつつ期待値を計算します。
状態とアクションを選択した時に、遷移し得る状態で得られる収益の期待値は、状態遷移確率を使って次のように表現できます。
これは、あるアクションを選択したときの収益の期待値なので、状態で選択し得る全てのアクションについて考慮することで状態での収益の期待値を表現できます。
状態のときにアクションを選択する確率である方策を使うと、次の式が得られます。
この式はベルマン方程式と呼ばれており、強化学習の重要な概念の1つです。
整理すると、ベルマン方程式は以下の要素から構成されています。
- : 確率的な方策
- : 状態遷移確率
- : からに遷移したときの報酬
- : 次のステップ以降の収益の期待値 割引率
また、同様の考え方で行動価値関数について計算すると、次のようになります。
CartPoleにあわせて簡易化する
#上記のベルマン方程式は、方策と状態遷移のいずれも確率的なものとしてモデリングしたものです。しかしCartPoleではアクションを実行した後の状態は一意に定まる(決定論的といいます)ので、この式を簡単にできます。
簡易化したバックアップ線図と行動価値関数は以下のようになります。
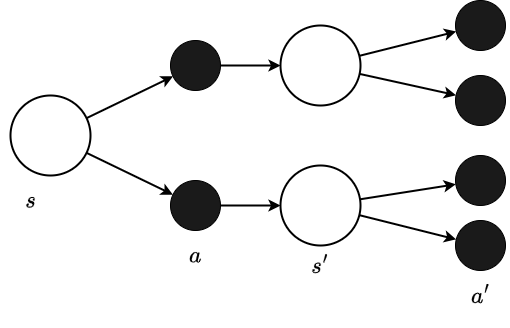
先ほどのバックアップ線図と異なり、アクションの後ろの状態が1つになっています。
行動価値関数を用いてアクションを選択する
#価値関数を導入した目的は、より収益が大きくなるアクションを選択するためでした。行動価値関数の出力は「ある状態でアクションを選んだときに得られる収益の期待値」を意味するため、どちらのアクションを選択すべきか判断できるようになりました。
このように状態価値の比較によってアクションを選択する方法は、あくまで強化学習の手法の1つの例です。
このような手法を価値ベースの手法といいます。
価値関数を部分的に可視化してみる
#価値関数について説明しましたが、より理解を深めるためにこの関数のグラフを考えてみたいと思います。ただし、全体を精確に把握するというよりは、ある状態を考えて、その状態での収益の期待値を考えます。
ここでは以下の2つの状態について考えます。
- ポールが安定して立っている状態
- ポールが倒れる直前の状態
まずポールが安定して立っている状態について考えます。これはつまり、この先のステップにおいても報酬を受取り続けられる状態です。収益の式を再掲します。
この式では報酬をステップ先まで足していますが、そのような収益が得られるのはエピソードが終了することなく続いた場合であり、それまでにポールが倒れた場合はそのステップまでの報酬を足した値が収益となります。ステップ先までの報酬が得られるとき、収益は以下のグラフのようになります。
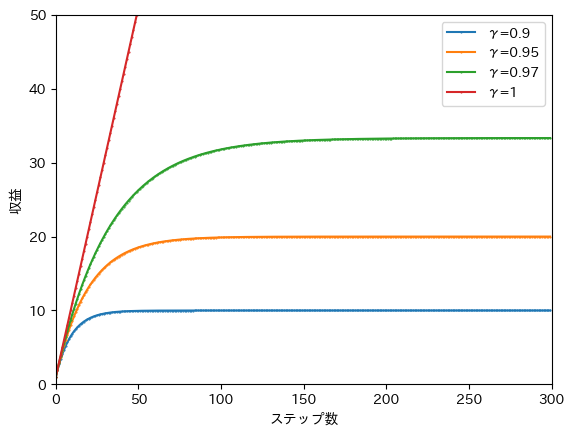
割引率の効果によって収益は集束します。そして集束する値は割引率によって異なります。
例えば割引率を採用した橙色の線を見ると、100ステップ以上エピソードが続くときの収益は20になることがわかります。
次にバランスを崩してエピソードが終了する直前の価値を確認します。下の図に示すように、ポール角度がエピソードの終了条件であるのラインの少し内側にあり、そのラインを超える方向に向かって大きな角速度がある状態を考えます。この状態から次の状態へ遷移します。なお、結果に影響はありませんが、アクションは50%でいずれかが選ばれるものとして計算します。
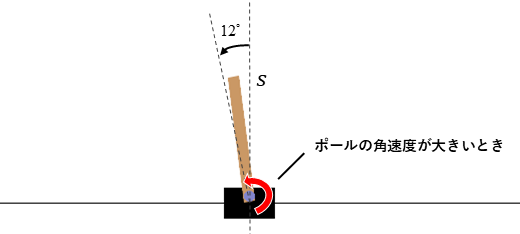
このときの状態価値を考えると次のようになります。
は次のステップの状態に遷移したときに与えられる報酬です。これはCartPoleの仕様ですが、遷移先の状態がエピソードの終了条件に当てはまっていても、報酬1を獲得します。次のステップ以降に獲得できる収益の期待値であるは0になります。これは選択したアクションによらずがエピソード終了条件にあてはまり、以降の状態遷移が行われないためです。その結果、上の図の状態の状態価値は1になります。
さて、本題である価値関数の形を考えます。ただし状態価値関数の引数である状態は4次元のベクトルであり、直観的な視覚化が難しいです。ここではざっくりとしたイメージをお伝えしたいので、ポール角度のみを変数とし、それ以外のカート位置・カート速度・ポール角速度は0で固定したときの収益のグラフを作成します。
割引率とすると、状態価値関数は次のようなグラフになります。[4]
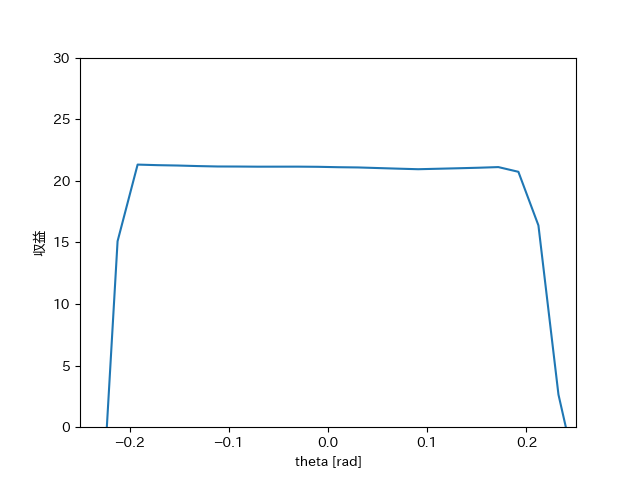
まず付近は、先ほど述べたようにポールが安定して直立している状態なので、収益は約20となります。また、エピソードの終了条件である付近では価値は下がっています。
行動価値関数をニューラルネットワークで近似する
#行動価値関数をCartPoleタスクに適用するにはさらに工夫が必要です。
先ほど示した式では、状態はで表されていましたが、CartPoleの状態は次のような4次元ベクトルで構成されます。(区別するためにボールドのを使って表記します。)
この状態を含む行動価値関数は次のように記述できます。
このように状態が複数の次元に渡る場合、行動価値関数を手動で定義することは困難になります。そのため、行動価値関数をニューラルネットワークで近似するというのが有名なDQN(Deep Q-Network)[5]のアイデアです。
Qネットワークとは、行動価値関数をニューラルネットワークに置き換えたものを指します。
DNNのアーキテクチャ
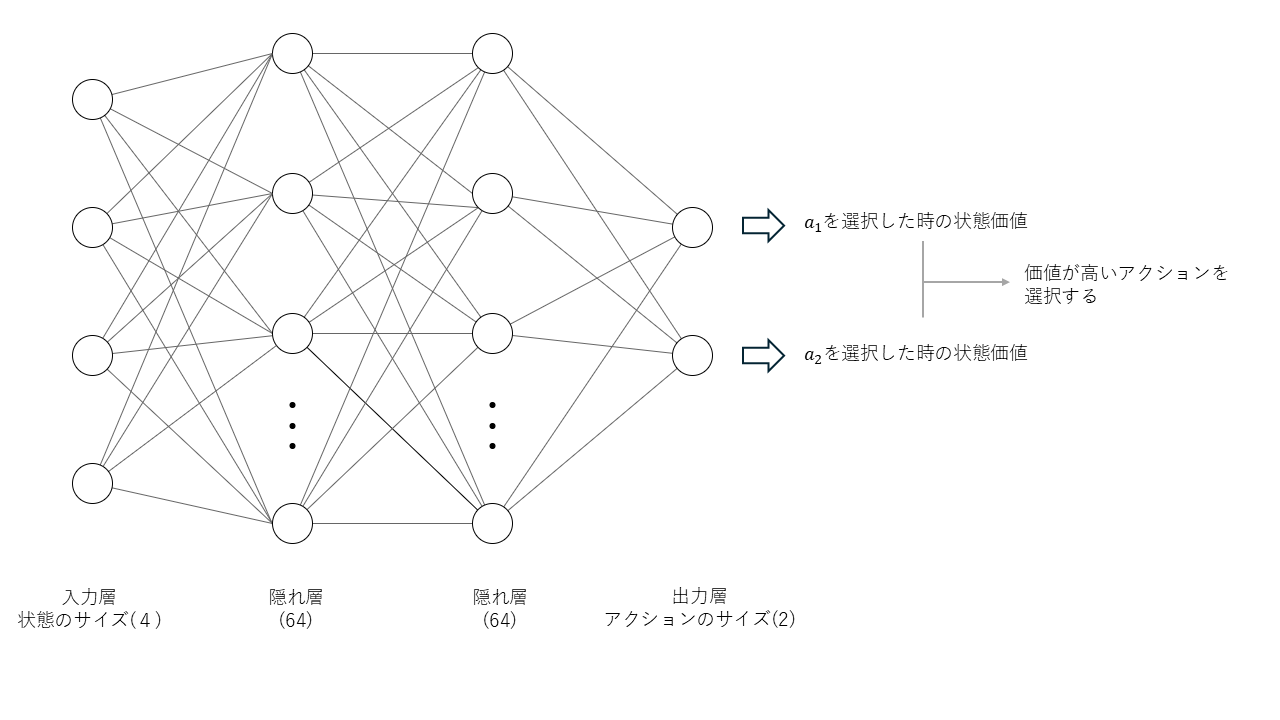
#今回は2つの隠れ層を持つDNNを使用します[6]。入力層には状態を入力するため4つのユニットを用意し、出力層のユニットはアクションの数と一致させます。出力層の各ユニットの値は、対応するアクションを選択したときの行動価値を意味し、この中から行動価値が最も高い行動を選択して実行します。
DNNの学習
#一般的に、ニューラルネットワークの学習にはデータセットが必要です。しかし強化学習ではあらかじめ用意されたデータセットを用意するのではなく、エージェントと環境の間でやり取りされたデータを使用します。
Qネットワークでも一般的なニューラルネットワークと同じく、損失関数を定義し、損失を最小化するという枠組みは変わりません。損失関数は、ターゲットと呼ばれる目標値と、現在の値を最小化する形で定義されます。
ここではターゲットと呼ばれ、以下で定義されます。
- : 行動 をとったときに得られる報酬
- : 価値が最大となるを選んだときの行動価値
学習の流れ
#これまでに説明した内容をまとめます。
- 以下の内容を学習完了まで繰り返します。
- エージェントは環境から初期状態を取得します。
- 以下を学習完了まで繰り返します。
- エージェントは(行動価値関数を使用して)状態からアクションを選択します。
- エージェントがアクションを実行することで、環境の状態が変化します。
- 環境はアクションの内容や遷移後の状態に応じて報酬をエージェントに返します。
- エージェントは保存した状態・アクション・報酬から、行動価値関数(Qネットワーク)を更新します。
DQNアルゴリズムを使用した学習の実践
#CartPoleタスクに取り組みます。なおこの記事で使用するソースコードは下記のリポジトリにアップロードしています。
クラス構造
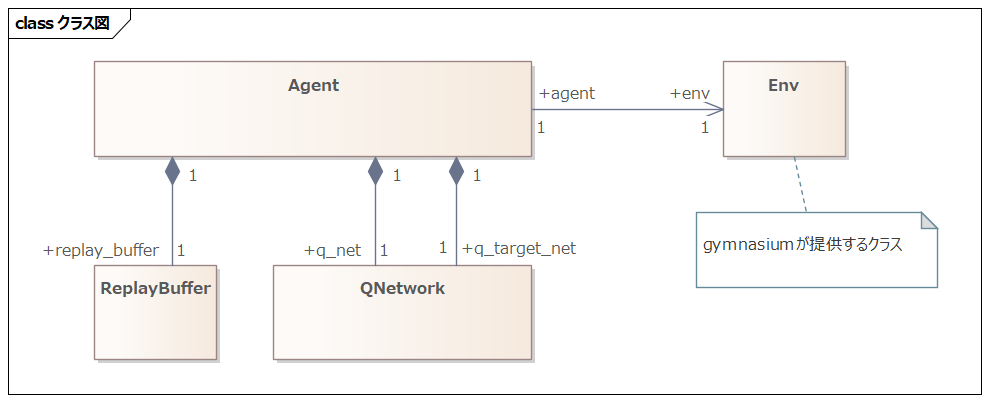
#冒頭に述べたように、CartPoleはGymnasiumという強化学習のライブラリに含まれているタスクです。Env(環境)クラスはGymnasiumが提供するものを使用するため、それ以外のクラスを実装します。
ReplayBufferクラスは、状態・アクション・報酬の履歴を保存するクラスです。エージェントはこのクラスに状態などの情報を保存し、Qネットワークを更新する際にデータを取り出します。
学習の実行と結果
#main.pyを実行すると学習を開始します。
from datetime import datetime
import gymnasium as gym
from agent import DQNAgent
# episode: エピソード数
episodes = 3000
# sync_interval: Q-networkを同期する間隔
sync_interval = 20
env = gym.make("CartPole-v1", render_mode="human")
# env = gym.make("CartPole-v1")
agent = DQNAgent("cpu")
reward_history = []
for episode in range(episodes):
observation, info = env.reset()
done = False
total_reward = 0.0
print("episode: ", episode)
while not done:
# 初期状態を渡し、行動を取得する
action = agent.get_action(observation)
# 環境を次のステップに進める
next_obs, reward, terminated, truncated, info = env.step(action)
agent.update(observation, action, reward, next_obs, terminated)
observation = next_obs
total_reward += reward
env.render()
if truncated or terminated:
print(" done : total_reward: ", total_reward)
print(" terminated: ", terminated, "truncated: ", truncated)
done = True
if episode % sync_interval == 0:
agent.sync_qnet()
postfix = datetime.now().strftime("%Y%m%d_%H%M%S")
agent.save_model(postfix)
学習の初期(~100エピソード)では、すぐにバランスを崩してエピソードが終了してしまいます。

ですが、その後も学習を続けると、うまくバランスを保てるようになります。
学習がうまく進んでいるかどうかを確認する1つの方法として、横軸にエピソード数、縦軸に累積報酬をとったグラフを確認する方法があります。学習が進むほど得られる累積報酬が増加するはずなので、右肩上がりなグラフが期待されます。サンプルとして3000エピソード学習した際のグラフを示します。
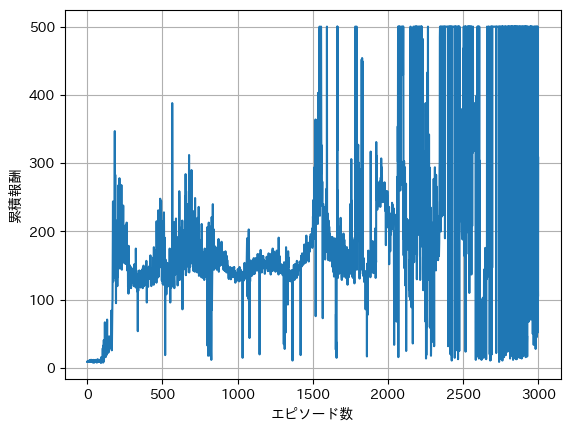
1500エピソードを超えたあたりで初めて500ステップに到達していることはわかりますが、エピソードが進んでも数十ステップで失敗しているエピソードもあります。現在の手法では-greeding法により最適ではないアクションを一定確率で選択するため、学習が進んでも早期に失敗することがあります。
この影響を取り除くため、3000エピソードの学習を20回行い、平均をとったものが以下のグラフです。
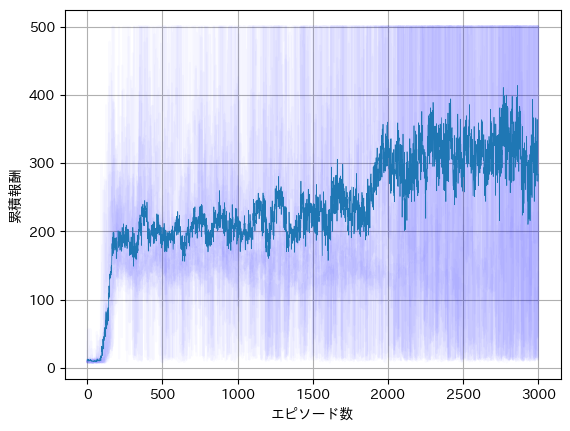
実線が20エピソードの平均で、個別のグラフを薄く表示しています。先ほどのグラフと比較すると、右肩上がりの傾向が見て取れます。
学習したモデルを保存する・利用する
#ここまでエージェントがいかにしてCartPoleタスクを学習するかについて説明しましたが、学習した結果を保存したり再利用する方法についても説明しておきます。今回の手法では、ニューラルネットワークが行動価値関数をうまく近似するパラメータを学習によって獲得したのでした。ですのでこのパラメータを保存しておけば学習結果の再利用が可能になります。
この学習済パラメータの保存方法はライブラリによって異なりますが、今回使用したpytorchでは次のような処理でパラメータをファイルに保存できます。
def save_model(self, postfix: str):
filename = f"q_net_{postfix}.pth"
torch.save(self.qnet, filename)
また学習時には、様々な状態を経験するために、一定確率でランダムなアクションを選択していました。
運用時には常に行動価値が高い行動を選択するよう変更します。
before(探索あり)
def get_action(self, state: np.ndarray) -> int:
if np.random.rand() < self.epsilon:
# ランダムに行動を選択(探索)
return np.random.choice(self.action_size)
else:
# Q値が最大となる行動を選択(活用)
state_as_tensor = torch.tensor(state[np.newaxis, :],dtype=torch.float32)
qs = self.qnet(state_as_tensor)
return qs.argmax().item()
after(探索なし)
def get_action(self, state: np.ndarray) -> int:
# Q値が最大となる行動を選択(活用)
state_as_tensor = torch.tensor(state[np.newaxis, :],dtype=torch.float32)
qs = self.qnet(state_as_tensor)
return qs.argmax().item()
探索を行わず、常に最適なアクションを選択するようになったエージェントは連続で500ステップの間生存するようになります。

さいごに
#この記事ではCartPoleタスクを題材にして、基本的な強化学習についてご紹介しました。
今回紹介した手法では状態を行動価値に変換する部分にニューラルネットを使用していますが、方策関数に使用したり、複数のネットワークを組み合わせて使用することもあります。また近年は、今回のような単純なネットワークではなく、LLMやVLMを使用する手法も生み出されています。実現したいタスクに応じて技術を組み合わせることが出来る点も強化学習のおもしろいところかなと思います。
参考資料
#Reinforcement Learning:An Introduction
Gymnasiumは強化学習のアルゴリズム開発や研究をサポートするシミュレーション環境を提供するPythonのライブラリです。 ↩︎
今回のように報酬が固定の値であれば、収益は等比数列の和と考えられるため、集束することが証明できます。 ↩︎
確率的な状態遷移の例としては、車のスリップがあります。「前進」というアクションを選択したとき、車の位置が変化するか、スリップして変化しないかは確率的な現象と考えることができます。 ↩︎
これは後述するDNNの出力を使用して作成したグラフです。 ↩︎
Deep Q-Network. https://arxiv.org/abs/1312.5602 ↩︎
DQNではネットワーク形状が特定の形に固定されているわけではありません。本記事では状態が4次元のベクトルとして与えられるため、全結合型のDNNを使用します。元論文ではゲームの画面から特徴を抽出するためにCNNが用いられています。 ↩︎