本記事は豆蔵デベロッパーサイトアドベントカレンダー2025第10日目の記事です。

0. はじめに

ロボット制御や画像処理の分野では、最適化問題を解く必要に迫られる場面が多々あります。
最適化問題といっても、線形計画法や組合せ最適化など、その種類や解法は多岐にわたります。
その中でも、実用上特によく扱われるのが「最小二乗問題」です。
これは、下記のような目的関数 $F(\boldsymbol{x})$ を最小化するパラメータ $\boldsymbol{x}$ を求める問題です。
（なお、一般的に $\boldsymbol{x}$ はベクトルとなります。）

\min_{\boldsymbol{x}} F(\boldsymbol{x}) = \frac{1}{2} \sum_{i} \| r_i(\boldsymbol{x}) \|^2

ここで、上式の $r_i(x)$ は残差（Residual）といい、観測されたデータ（=実測値） $y_i$ と予測値（=理論値） $f_i(x)$ との差を意味します。

r_i(\boldsymbol{x}) = y_i - f_i(\boldsymbol{x})

今回は、このような非線形最小二乗問題を効率的に解くためのGoogle社製ソルバ "Ceres Solver"について紹介します。

1. 本記事の環境について

本記事ではUbnutu 24.04を対象とします。
筆者の環境ではWSL2を利用していますが、純正のUbuntuでも問題ありません。

Information

本記事ではUbuntu環境でライブラリを使用していますが、Windowsでも動作します。
詳しくは下記リンク先をご覧ください。
http://ceres-solver.org/installation.html#windows

2. 環境構築

CeresSolverを使用するための前準備です。少し長いですがお付き合いください。

必要なライブラリのインストール

まずは、Ceres Solverのビルドに必要なツールをインストールします。
下記を1行ずつ実施して、インストールしてください。

# apt update（パスワード入力を求められます）
sudo apt update && sudo apt upgrade -y
# ビルドツール
sudo apt install build-essential
# Git
sudo apt install git
# CMake
sudo apt install cmake
# google-glog + gflags
sudo apt install libgoogle-glog-dev libgflags-dev
# Use ATLAS for BLAS & LAPACK
sudo apt install libatlas-base-dev
# Eigen3
sudo apt install libeigen3-dev
# SuiteSparse (optional)
sudo apt install libsuitesparse-dev

ワークスペース作成

次に、任意の場所にワークスペースを作成しましょう。
今回はホームディレクトリにceres_solver_wsというディレクトリを作成します。

mkdir ~/ceres_solver_ws

Information

一般的なLinux環境での"~"（チルダ）は、ホームディレクトリを意味します。
ホームディレクトリの絶対パスは/home/${ユーザ名}/です。

CeresSolverライブラリのクローン

ワークスペースが作成出来たら、CeresSolverのソースをクローンしましょう。
クローンする場所は任意ですが、今回はexternalディレクトリ内にクローンしておきます。
この時、Submoduleについても再帰的に取得する必要があるため、--recursiveオプションを付与する必要がある点に注意してください。

cd ~/ceres_solver_ws
mkdir external
cd external
git clone --recursive https://github.com/ceres-solver/ceres-solver

Information

サブモジュールも再帰的に取得するコマンドとして、--recurse-submodulesオプションも存在するようです。

git clone --recurse-submodules ${repo-url}

CeresSolverライブラリのビルド&インストール

クローンが出来たら、CMakeを使用してビルドします。

# CeresSolverのソースに移動
cd ceres-solver
# ビルド用のディレクトリを作成
mkdir build
# ビルドシステムの生成（out-of-sourceビルド）
cmake -S . -B build
# ビルド実行
cmake --build build

ビルドシステム生成時にエラーが発生する場合

コマンド実施に下記のエラーが発生した場合は、build-essentialパッケージをaptでインストールしてください。

CMake Error at CMakeLists.txt:33 (project):
  No CMAKE_CXX_COMPILER could be found.

  Tell CMake where to find the compiler by setting either the environment
  variable "CXX" or the CMake cache entry CMAKE_CXX_COMPILER to the full path
  to the compiler, or to the compiler name if it is in the PATH.

-- Configuring incomplete, errors occurred!

並列ビルドによる高速化

ビルドには少し時間がかかります。下記コマンドで並列ジョブを使用して高速化可能です。
nprocコマンドは「システムが利用可能なCPUコア数を取得する」コマンドです。
この出力結果が$(nproc)と置換されます。

cmake --build build -- -j$(nproc)

下記のように達成率が100%となるようなログが出力されれば、ビルド成功です。

[ 99%] Built target robot_pose_mle
[ 99%] Building CXX object examples/sampled_function/CMakeFiles/sampled_function.dir/sampled_function.cc.o
[ 99%] Linking CXX executable ../../bin/sampled_function
[ 99%] Built target sampled_function
[ 99%] Building CXX object examples/slam/pose_graph_2d/CMakeFiles/pose_graph_2d.dir/pose_graph_2d.cc.o
[ 99%] Linking CXX executable ../../../bin/pose_graph_2d
[ 99%] Built target pose_graph_2d
[ 99%] Building CXX object examples/slam/pose_graph_3d/CMakeFiles/pose_graph_3d.dir/pose_graph_3d.cc.o
[100%] Linking CXX executable ../../../bin/pose_graph_3d
[100%] Built target pose_graph_3d

最後に、ビルドした生成物をインストールします。
インストール先のデフォルトは/usr/localです。

# ビルドした生成物をインストールする
sudo cmake --install build

インストールが完了したら、念のために下記のコマンドを実施しておきましょう。

source ~/.bashrc

3. 簡単な最適化計算を解いてみる

CMakeLists.txtとソースファイルの作成

では、CeresSolverを実際に使用して最適化問題を解いてみましょう。

まずは，ワークスペース~/ceres-solver_wsに戻り、CMakeLists.txtファイルを作成します。

cd ~/ceres_solver_ws
touch CMakeLists.txt

CMakeLists.txtには下記を記述します。
エディタは自由ですが、今回はVisual Studio Codeを使用しています。
（WSLとの相性も良いのでVSCodeはおすすめ！）

# CMakeの最低バージョン指定
cmake_minimum_required(VERSION 3.14)

# プロジェクト名定義
project(ceres-solver-sample)

# 実行ファイルをビルドディレクトリ直下に出力するように設定
# （不要な場合は削除してください）
set(CMAKE_RUNTIME_OUTPUT_DIRECTORY ${CMAKE_BINARY_DIR})

# 依存パッケージ指定
find_package(Ceres REQUIRED)

# サブディレクトリ追加
add_subdirectory(src)

次に，srcディレクトリを作成します。
srcディレクトリ内にもCMakeLists.txtを作成します。

cd ~/ceres-solver_ws
mkdir src
cd src
touch CMakeLists.txt

src/CMakeLists.txtには下記のように記述します。

# simple-ols
add_executable(simple-ols simple-ols.cpp)
target_link_libraries(simple-ols absl::log_initialize Ceres::ceres)

最後に，計算を記述するC++ファイル（simple-ols.cpp）を作成します。
先述したCMakeLists.txtに記載したファイル名と合致するようにしてください。

touch simple-ols.cpp

最終的なファイル構造は下記のようになります。

ceres_solver_ws/
├── CMakeLists.txt
└── src/
    ├── CMakeLists.txt
    └── simple-ols.cpp

最適化計算の実装

作成したsimple-ols.cppに処理を記述しましょう。

今回のお題としては，下式で定義された関数 $f(x)$ の値を最小化する $x$ を求めてみます。

f(x) = \frac{1}{2} (5 - x)^2

$x=5$ で最小値を取ることは火を見るよりも明らかですが，これをプログラムで求めてみましょう。
実装コードは下記です。

simple-ols.cpp

#include <ceres/ceres.h>
#include <glog/logging.h>

using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;

/// @brief 残差の構造体
/// @remark 最適化の対象を()演算子にて記述します
struct CostFunctor
{
    template <typename T>
    bool operator()(const T* const x, T* residual) const
    {
		// 今回の最適化対象式
        residual[0] = T(5.0) - x[0];
        return true;
    }
};

/// @brief メイン関数
int main(int argc, char** argv)
{
	// 初期値の定義
    double initial_x = 1.0;
    double x = initial_x;

	// コスト関数の定義
	CostFunction* cost_function = new ceres::AutoDiffCostFunction<CostFunctor, 1, 1>();

	// 最適化問題の定義
    Problem problem;
	problem.AddResidualBlock(cost_function, nullptr, &x);	// 残差ブロックを追加
	problem.SetParameterLowerBound(&x, 0, 0.0);		// 入力パラメータの下限値設定
	problem.SetParameterUpperBound(&x, 0, 10.0);	// 入力パラメータの上限値設定

    // 計算オプションの定義
    ceres::Solver::Options options;
    options.linear_solver_type = ceres::DENSE_QR;	// 密行列でのQR分解を使用する
    options.minimizer_progress_to_stdout = true;	// 進捗出力を有効化
	options.max_num_iterations = 10; // 最大反復回数
    
	// 計算結果の定義
	Solver::Summary summary;

	// 最適化計算を行う
    ceres::Solve(options, &problem, &summary);

	// 計算結果の出力
	// 計算結果は変数xに格納されます
    std::cout << summary.BriefReport() << std::endl;
    std::cout << "x: " << initial_x << " -> " << x << std::endl;

    return 0;
}

プログラムの詳細

コードの中で重要な部分について説明します。

コスト定義

/// @brief コスト構造体
/// @remark 最適化の対象を()演算子にて記述します
struct CostFunctor
{
    template <typename T>
    bool operator()(const T* const x, T* residual) const
    {
		// 今回の最適化対象式
        residual[0] = T(5.0) - x[0];
        return true;
    }
};

今回の最適化の対象となる式を記述します。

()演算子の中に計算式を記述する必要があります。
テンプレートTには、最適化計算時に使用される型が使用されます。
- 具体的には、ceres::Jet型というデータ型が使用されます。
- double型などを使用する場合は、T型でキャストする必要がある点に注意してください

コスト関数の定義

// コスト関数の定義
CostFunction* cost_function = new ceres::AutoDiffCostFunction<CostFunctor, 1, 1>();

上記にはコスト関数の定義を行っています。今回は計算で自動微分（Automatic Differentiation）を使用するように設定しています。
また、テンプレート引数のそれぞれの意味は下記の通りです。

第1引数: コスト関数の構造体型
第2引数: 誤差パラメータの次元数
第3引数: 最適化パラメータの次元数

今回のお題では、誤差パラメータの次元(= $f(x)$ の次元）はスカラーのため1、最適化パラメータ $x$ の次元は同じくスカラー量のため1となります。

最適化問題の定義

// 最適化問題の定義
Problem problem;
problem.AddResidualBlock(cost_function, nullptr, &x);	// 残差ブロックを追加
problem.SetParameterLowerBound(&x, 0, 0.0);		// 入力パラメータの下限値設定
problem.SetParameterUpperBound(&x, 0, 3.0);	// 入力パラメータの上限値設定

最適化問題を定義します。
また、入力パラメータの上限値、下限値もここで設定します。

AddResifualBlockメソッドの第2引数は損失関数（Loss Function）を定義できます。
本記事では詳細を割愛しますが、詳細は下記リンク先をご覧ください。
http://ceres-solver.org/nnls_tutorial.html#robust-curve-fitting

ビルドと実行

CMakeを使用して作成したプログラムをビルドします。

cd ~/ceres_solver_ws
cmake -S . -B bin
cmake --build bin

ビルドが成功したら、下記のコマンドで実施してみましょう。

./bin/simple-ols

これを実施すると、下記のようなログが出力されます。

iter      cost      cost_change  |gradient|   |step|    tr_ratio  tr_radius  ls_iter  iter_time  total_time
   0  8.000000e+00    0.00e+00    4.00e+00   0.00e+00   0.00e+00  1.00e+04        0    1.35e-05    4.40e-05
   1  7.998400e-08    8.00e+00    4.00e-04   0.00e+00   1.00e+00  3.00e+04        1    8.09e-05    1.88e-04
   2  8.886518e-17    8.00e-08    1.33e-08   4.00e-04   1.00e+00  9.00e+04        1    3.24e-05    2.39e-04
Ceres Solver Report: Iterations: 3, Initial cost: 8.000000e+00, Final cost: 8.886518e-17, Termination: CONVERGENCE
x: 1 -> 5

最終行のログより、最適入力値は5であると計算できました。
また、最適入力値の場合の残差コスト（Final cost）は8.886518e-17であり、ほぼ0であることも計算できました。

入力パラメータの上下限値を変えてみる

次に、入力値の範囲を1~3に変更して計算してみましょう。
下記の★印部分の値を10から3に変更します。

// 最適化問題の定義
Problem problem;
problem.AddResidualBlock(cost_function, nullptr, &x);	// 残差ブロックを追加
problem.SetParameterLowerBound(&x, 0, 0.0);	// 入力パラメータの下限値設定
problem.SetParameterUpperBound(&x, 0, 3.0);	// 入力パラメータの上限値設定（★）

これを再度ビルドして実行してみると、最適入力は $x=3$ 、残差コストは2.000000e+00となります。
指定した制約内でコストが最小となるような最適入力が求められることが確認できます。
参考のため、計算ログを下記に記します。

iter      cost      cost_change  |gradient|   |step|    tr_ratio  tr_radius  ls_iter  iter_time  total_time
   0  8.000000e+00    0.00e+00    2.00e+00   0.00e+00   0.00e+00  1.00e+04        0    1.21e-05    4.23e-05
   1  2.000000e+00    6.00e+00    0.00e+00   0.00e+00   7.50e-01  1.14e+04        1    6.80e-05    1.66e-04
Ceres Solver Report: Iterations: 2, Initial cost: 8.000000e+00, Final cost: 2.000000e+00, Termination: CONVERGENCE
x: 1 -> 3

4. 4自由度平面マニピュレータの逆運動学を数値的に解いてみる

3章では入力パラメータとコストがともにスカラー量である最適化問題を解くサンプルを紹介しました。
本章では、より難しい非線形最適化問題のお題として「4自由度平面マニピュレータの逆運動学」を解いてみましょう。

4自由度平面マニピュレータとは

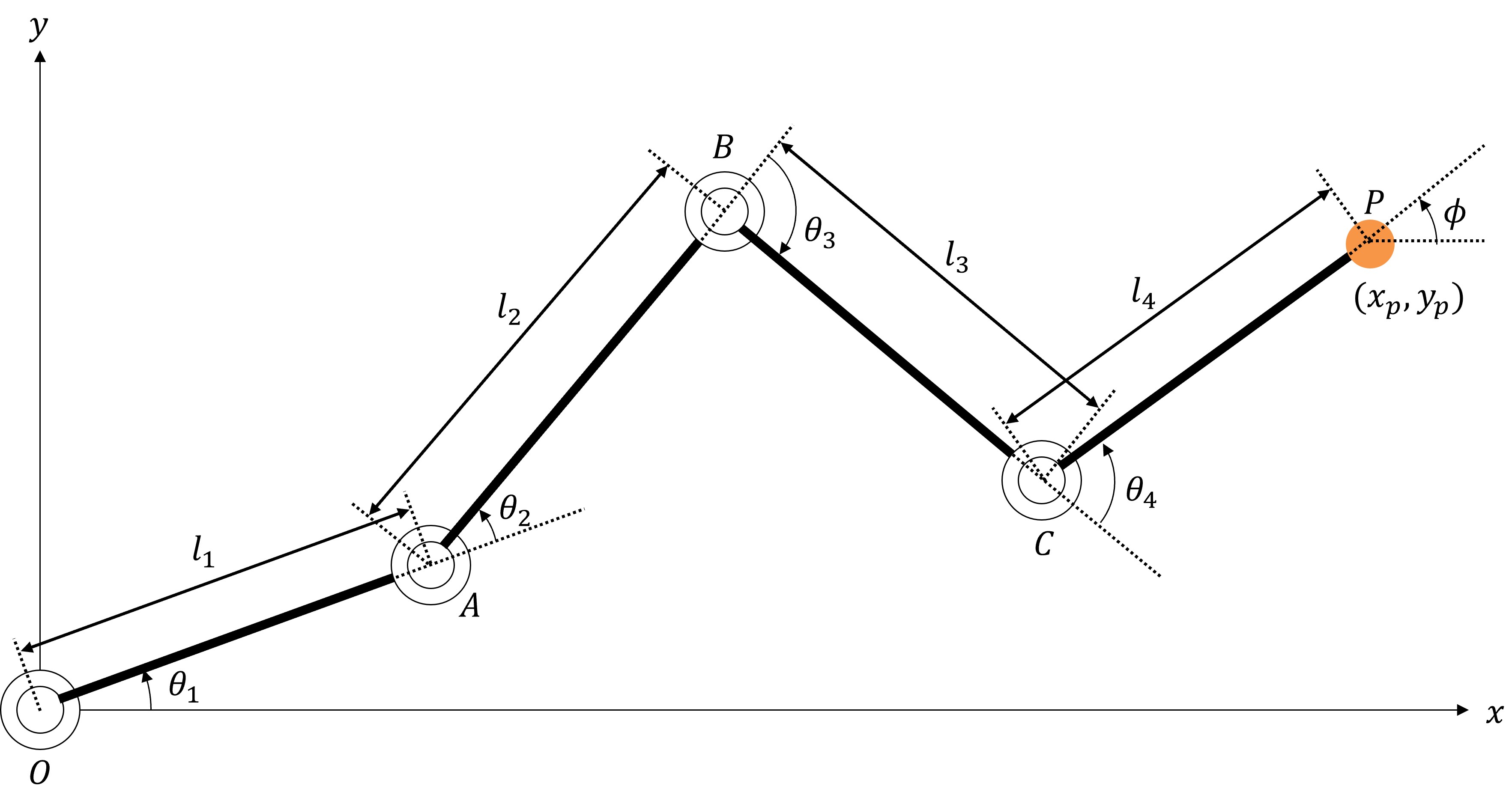
下図のような4つの関節を持つ平面マニピュレータを対象に、逆運動学計算を実装してみます。
パラメータについては下記の通りとします。

各リンク長は $L_i$ とする
各関節角度の回転角度を $\theta_i$ $θ_{i}$ とする
- $i=1,2,3,4$
各関節の回転正方向は「反時計回り（ccw）」とする
ロボットの先端（点P）のX座標を $x_p$ 、Y座標を $y_p$ とする
ロボットの先端の姿勢角度（半直線CPとX軸のなす角）を $\phi$ とする

順運動学計算

対象ロボットの各軸角度 $\boldsymbol{\theta}$ と先端位置 $\boldsymbol{p}$ の関係を考えてみましょう。
ここで、それぞれのベクトルの定義は下記とします。

\boldsymbol{\theta} = \begin{bmatrix} \theta_1 \\ \theta_2 \\ \theta_3 \\ \theta_4 \end{bmatrix}

\boldsymbol{p} = \begin{bmatrix} x_p \\ y_p \\ \phi \end{bmatrix}

上図での原点Oから点Aまでのベクトル $\vec{OA}$ は下記のように記述できます。

\vec{OA} = \begin{bmatrix} l_1 \cos \theta_1 \\ l_1 \sin \theta_1 \end{bmatrix}

これと同様に、点Aから点B、点Bから点C、点Cから点Pまでのベクトルはそれぞれ下記のようになります。

\vec{AB} = \begin{bmatrix} l_2 \cos(\theta_1 + \theta_2) \\ l_2 \sin(\theta_1 + \theta_2) \end{bmatrix}

\vec{BC} = \begin{bmatrix} l_3 \cos(\theta_1 + \theta_2 + \theta_3) \\ l_3 \sin(\theta_1 + \theta_2 + \theta_3) \end{bmatrix}

\vec{CP} = \begin{bmatrix} l_4 \cos(\theta_1 + \theta_2 + \theta_3 + \theta_4) \\ l_4 \sin(\theta_1 + \theta_2 + \theta_3 + \theta_4) \end{bmatrix}

これらを合わせると、XY平面上での点Pの座標は下記のようになります。
（式が長くなるためベクトル表記のままとしています）

\begin{bmatrix} x_p \\ y_p \end{bmatrix} = \vec{OA} + \vec{AB} + \vec{BC} + \vec{CP}

また、ロボット先端の姿勢角度 $\phi$ は下記のようになります。

\boldsymbol{\phi} = \theta_1 + \theta_2 + \theta_3 + \theta_4

上式2つを合わせ、関節角度ベクトル $\boldsymbol{\theta}$ から先端位置ベクトル $\boldsymbol{p}$ への写像を $f$ と定義すると、下式のように表現できます。

\boldsymbol{p} = f(\boldsymbol{\theta})

これがロボットの順運動学計算時に使用する式となります。

逆運動学計算

一方、逆運動学（Inverse Kinematics）は文字通り順運動学の逆を意味します。
つまり、 $f$ の逆関数（=先端位置 $\boldsymbol{p}$ から関節角度 $\boldsymbol{\theta}$ への写像）を求める操作となります。

\boldsymbol{\theta} = f^{-1}(\boldsymbol{p})

一般的に順運動学よりも逆運動学計算の方が計算量が多くなります。
ロボットの機構次第では解析的に解くことも可能ですが、一般的に自由度が多くなるほど逆運動学計算の難易度は難しくなります。
今回はこの計算をCeresSolverを使って数値的に解いてみます。

コード実装

ディレクトリとCMakeLists.txtの作成

srcディレクトリ直下に本問題を解くためのファイルを格納するディレクトリを作成します。
ディレクトリ名は4dof-ikとします。

cd ~/ceres_solver_ws/src
mkdir 4dof-ik
cd 4dof-ik
touch CMakeLists.txt

作成した4dof-ikディレクトリもサブディレクトリとして登録されるように、srcディレクトリ直下のCMakeLists.txtに下記を記載します。（最終行を追加してください）

# simple-ols
add_executable(simple-ols simple-ols.cpp)
target_link_libraries(simple-ols absl::log_initialize Ceres::ceres)

# 4dof-ikディレクトリをサブディレクトリとして登録する
add_subdirectory(4dof-ik)

データ構造体の定義

まずはデータ構造をまとめるための構造体を定義します。
4dof-ikディレクトリ内に、位置と姿勢をまとめたPose構造体と、ロボットの機構パラメータをまとめたKinematicsParameters構造体を作成します。

cd ~/ceres_solver_ws/src/4dof-ik
touch Pose.hpp
touch KinematicsParameters.hpp

下記のように記述します。

Pose.hpp

/// @brief 姿勢
struct Pose
{
    /// @brief X座標
    double x; 

    /// @brief Y座標
    double y;

    /// @brief 先端角度
    double phi;

    Pose(double x_, double y_, double phi_)
        : x(x_), y(y_), phi(phi_){}
};

KinematicsParameters.hpp

/// @brief 機構パラメータ (リンク長)
struct KinematicParameters {
    /// @brief 第1リンク長
    double L1; 

	/// @brief 第2リンク長
    double L2;

	/// @brief 第3リンク長
    double L3;

	/// @brief 第4リンク長
    double L4;

    /// @brief コンストラクタ
    /// @param l1 第1リンク長
    /// @param l2 第2リンク長
    /// @param l3 第3リンク長
    /// @param l4 第4リンク長
    KinematicParameters(double l1, double l2, double l3, double l4)
        : L1(l1), L2(l2), L3(l3), L4(l4) {}
};

最適化計算の実装

次に、逆運動学計算を解くためのメインプログラムを作成します。

メインプログラム作成

touch 4dof-ik.cpp

最終的なファイル構造は下記のようになります。

ceres_solver_ws/
├── CMakeLists.txt
└── src/
    ├── CMakeLists.txt
    ├── simple-ols.cpp
    └── 4dof-ik/
        ├── CMakeLists.txt
        ├── 4dof-ik.cpp
        ├── KinematicsParameters.hpp
        └── Pose.hpp

4dof-ik.cppの実装は下記の通りです。

4dof-ik.cpp

#include <iostream>
#include <ceres/ceres.h>
#include <ceres/rotation.h>
#include <cmath>
#include "Pose.hpp"
#include "KinematicsParameters.hpp"

/// @brief 順運動学を行う
/// @tparam T データ型
/// @param[in] kp 機構パラメータ
/// @param[in] theta 関節角度ベクトル（配列）
/// @param[out] x X座標
/// @param[out] y Y座標
/// @param[out] phi 先端角度
template <typename T>
void compute_forward_kinematics(const KinematicParameters& kp, const T* const theta, T& x, T& y, T& phi)
{
    x = T(kp.L1) * cos(theta[0])
      + T(kp.L2) * cos(theta[0] + theta[1])
      + T(kp.L3) * cos(theta[0] + theta[1] + theta[2])
      + T(kp.L4) * cos(theta[0] + theta[1] + theta[2] + theta[3]);

    y = T(kp.L1) * sin(theta[0])
      + T(kp.L2) * sin(theta[0] + theta[1])
      + T(kp.L3) * sin(theta[0] + theta[1] + theta[2])
      + T(kp.L4) * sin(theta[0] + theta[1] + theta[2] + theta[3]);

    phi = theta[0] + theta[1] + theta[2] + theta[3];
}

/// @brief コスト
struct IKCostFunction
{
    Pose target_pose;
    KinematicParameters kp;

    /// @brief コンストラクタ
    /// @param pose 先端位置・姿勢
    /// @param param 機構パラメータ
    IKCostFunction(const Pose& pose, const KinematicParameters& param)
        : target_pose(pose), kp(param)
    {
    }

    template<typename T>
    bool operator()(const T* const theta, T* residuals) const
    {
		T x, y, phi;
		compute_forward_kinematics(kp, theta, x, y, phi);

        residuals[0] = T(target_pose.x) - x;	// X座標誤差
        residuals[1] = T(target_pose.y) - y;	// Y座標誤差
        residuals[2] = T(target_pose.phi) - phi;	// 姿勢角度誤差

        return true;
    };
};

/// @brief メイン関数
int main(int argc, char** argv)
{
    // 機構パラメータの定義
    double l1 = 1.5;
    double l2 = 1.5;
    double l3 = 1.0;
    double l4 = 1.0;

    // 目標位置・姿勢の定義
    double x_target = 3.2;
    double y_target = 0.8;
    double phi_target = -M_PI_4;

    // 初期値の設定
    double theta[4] = {0.0, 0.0, 0.0, 0.0};
    KinematicParameters kp(l1, l2, l3, l4);
    Pose target_pose{ x_target, y_target, phi_target };

    // 最適化問題の定義
    ceres::Problem problem;
    problem.AddResidualBlock(
		// 誤差次元数は3、最適化変数次元数は4
        new ceres::AutoDiffCostFunction<IKCostFunction, 3, 4>(
            new IKCostFunction(target_pose, kp)
        ),
        nullptr,
        theta
    );

    // 上下限値の適用（-pi ~ piとする）
    for (int i = 0; i < 4; i++)
    {
        problem.SetParameterLowerBound(theta, i, -M_PI);
        problem.SetParameterUpperBound(theta, i, M_PI);
    }

    // ソルバ設定
    ceres::Solver::Options options;
    options.linear_solver_type = ceres::DENSE_QR;
    options.minimizer_progress_to_stdout = true;
    options.max_num_iterations = 100; // 最大反復回数
    options.function_tolerance = 1e-6; // 収束判定の閾値

    // 最適化計算を解く
    ceres::Solver::Summary summary;
    ceres::Solve(options, &problem, &summary);

	// 計算結果の出力
    std::cout << summary.BriefReport() << std::endl;
    if (summary.termination_type == ceres::CONVERGENCE)
    {
        std::cout << "✅ IK Solution Found! (Final Cost: " << summary.final_cost << ")\n";
    } 
    else
    {
        std::cout << "❌ IK Failed to Converge.\n";
    }

    // 求まった関節角度の出力
    std::cout << "theta[0] = " << theta[0] << std::endl;
    std::cout << "theta[1] = " << theta[1] << std::endl;
    std::cout << "theta[2] = " << theta[2] << std::endl;
    std::cout << "theta[3] = " << theta[3] << std::endl;

	// 求めた関節角度でどの位置・姿勢になるかを確かめる
    std::cout << "Check Forward kinematics calculation:" << std::endl;
	double x_result, y_result, phi_result;
	compute_forward_kinematics(kp, theta, x_result, y_result, phi_result);
    std::cout << "x   = " << x_result << std::endl;
    std::cout << "y   = " << y_result << std::endl;
    std::cout << "phi = " << phi_result << std::endl;
    return 0;
}

CMakeLists.txtに追加する

4dof-ikディレクトリ内のCMakeLists.txtに下記を記述します。

4dof-ik/CMakeLists.txt

# 4dof-ik
add_executable(4dof-ik 4dof-ik.cpp)
target_link_libraries(4dof-ik absl::log_initialize Ceres::ceres)

ビルド・実行

ワークスペースに移動してビルドします。

cd ~/ceres_solver_ws
cmake --build bin

実行してみます。

./bin/4dof-ik

実行結果は下記のようになると思います。
（イテレーション結果は割愛します）

Ceres Solver Report: Iterations: 7, Initial cost: 2.248425e+00, Final cost: 4.808292e-20, Termination: CONVERGENCE
✅ IK Solution Found! (Final Cost: 4.80829e-20)
theta[0] = -0.414376
theta[1] = 1.25568
theta[2] = 0.609086
theta[3] = -2.23579
Check Forward kinematics calculation:
x   = 3.2
y   = 0.8
phi = -0.785398

最終コストはほぼ0のため、指定した目標位置・姿勢を満たす関節角度を見つけることが出来ました！
また、検算結果も正しそうです！

5. おわりに

本記事では、CeresSolverを使用して最適化問題を解くプログラムを紹介しました。
本記事で紹介したサンプル以外にも、公式ページでは多くのサンプルプログラムが提供されています。
興味のある方は確認してみてください。
http://ceres-solver.org/nnls_tutorial.html#non-linear-least-squares

また、今回作成したプログラムは、下記のリポジトリで公開しています。
https://github.com/hayat0-ota/CeresSolver_tutorial