要注意!統計的検定にはびこる誤解
Back to Topはじめに
#こんにちは。教育グループの高です。
最近、研修の中で統計学について取り扱うことがありました。その際、統計的検定について世間一般ではかなり誤解されていることが分かりました(かくゆう私も、研修準備をしている中で、誤解していることがあることに気が付きました...)。
統計的検定は、統計以外を専門とする研究者であっても誤解していることが多いです。そのため、一部学会では以下のような動きがあります(記事のタイトルはいずれもP値となっていますが、中身は統計的検定について言及されています)。
P値の誤用の蔓延に米国統計学会が警告
T&F社のBASP誌がP値の使用禁止を発表
今回は、統計的検定にありがちな「誤解」について書いてみたいと思います。
統計的検定の「誤解」
#その1:統計的検定で優劣を評価することができる
#それ、誤解です。
例えば2標本のt検定の場合、「2標本の平均値に差がある」あるいは「2標本の平均値に差があるとはいえない」のどちらかの結論を導くことになります。
逆に言うと、統計的検定ではそれ以上のことは言えません。P値の値がどれだけ大きかろうが、どれだけ大きかろうが、優劣を判断するためには使えません。
あくまでも「差があるかどうか」を示すのが統計的検定です。優劣を評価するためには、別の指標(システムが評価対象であれば、効率やコスト等)をあわせて議論する必要があります。
その2:P値が有意水準以下になるということは、帰無仮説が間違っている
#それ、半分誤解です。
もちろん帰無仮説が間違っているケースもあるのですが、帰無仮説以外の仮定が間違っている可能性もなくはありません。
一番分かりやすい例が、標本の取り方です。標本は完全ランダムに採取できているのでしょうか?標本の採取に偏りはありませんか?例えば、選挙の当選予測を考えてみましょう。ある候補者のお膝元の地区の投票所だけで出口調査をした結果、完全ランダムと言えるでしょうか?
また、パラメトリック検定では、母集団が正規分布であることを仮定しています。たとえ母集団が正規分布していない、しているかどうかわからない場合でも、標本数が十分であれば中心極限定理を後ろ盾として検定を行うことがあります。
中心極限定理は本当に成り立っているでしょうか?そもそもの標本数が少ないと中心極限定理が成り立ちません。また、分布の裾が極端な値の分布(重尾分布[1])だと、中心極限定理の適用が難しかったりします。
その3:標本(データ)数が多ければ大丈夫!
#それ、誤解です。
標本数が多くなればなるほど、P値の値は小さくなる傾向になります。つまり、「統計的検定において帰無仮説を棄却しやすくなる状況にできる」ということです。2標本のt検定の場合でいうと、「平均値に差がある」という結論を恣意的に導けてしまいます。
こんなシミュレーションをしてみました。
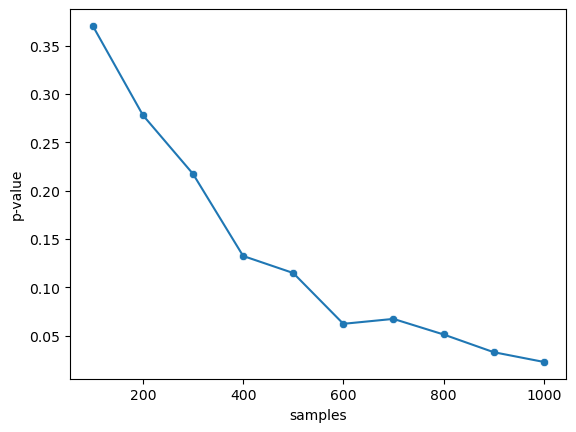
- 平均100.5、標準偏差5に従う母集団から、標本を取り出し、「平均値が100と等しい」かどうかを確かめるため、1標本のt検定を行う
- 標本数は100~1000の10通り(100刻み)とし、各標本数に対して1000回試行(標本抽出、検定)を行う
P値の平均値を求めたグラフが以下の通りです。どうでしょう。標本数を増やすごとにP値の値が小さくなっていきます。有意水準には依存しますが、標本数を非常に大きくすれば、棄却仮説を簡単に棄却できてしまうのです。
ついつい標本数が多ければ良いと考えがちですが、それが統計的検定として正しいかどうかはまた別の話です。
おわりに
#今回は、統計的検定についてよくある誤解について執筆してみました。
個人的には、統計的検定は、適用する分野によって注意する部分が異なると思います。我々IT業界であれば、IoTやITシステム化により、非常に多くの情報を取得できます。そのことが、かえって統計的検定の誤解(特に誤解その3)を招くことにもなりかねません。
もし統計的検定を使う機会があれば、本記事の内容が参考になれば幸いです。
さいごに
#今回は、以下の情報も参考に執筆しております。
- American Statistical Association(ASA), AMERICAN STATISTICAL ASSOCIATION RELEASES STATEMENT ON
STATISTICAL SIGNIFICANCE AND P-VALUES, https://www.amstat.org/asa/files/pdfs/p-valuestatement.pdf, 最終アクセス日:2023/12/28 - 日本計量生物学会, 統計的優位性とP値に関するASA声明, https://www.biometrics.gr.jp/news/all/ASA.pdf, 最終アクセス日:2023/12/28
- ASAの記事の翻訳版です
代表的なものにパレート分布があります。パレート分布の具体例としては、富の分布があります(社会全体の8割の富が2割の富裕層に集中し、残り2割の富を8割の低所得者で分け合う)。このような極端な分布では、分布の特徴を表す平均値や分散の意味が薄れます。 ↩︎