選択された結果を分析する(2項検定)
Back to Top皆さんは仕事やプライベートで「アンケート」への回答を求められた経験をお持ちだと思います。
アンケート回答方法としては複数の選択肢から選ぶもの、点数を付けるものなど様々でしょう。
回答する側から言わせてもらえれば、手間のかかるアンケートだと回答する気力が失せるので、回答の選択肢が「はい・いいえ」くらいの簡単なアンケートの方が応えやすいですね。
過去、大手フリマサイトの購入者・出品者の評価は「良い・普通・悪い」からの3択でしたが、現在は「良い・悪い」の2択になっているようです。
仕事や生活で周りを見渡してみると意外と「2択」が多いことに気が付きます。
「有るのか・無いのか」「するのか・しないのか」「出来たのか・出来なかったのか」などなど。
目の前に示された”選択の結果”が従来のパターンと違っているのかが分かれば、その後の判断材料になるでしょう。
今回は2択の結果を検定する方法「2項検定」をjamoviを使って説明していきます。
2項検定とは
#選択肢が「はい」と「いいえ」のように2つしか存在しない変数(2値変数)について,「はい」と「いいえ」の比率が想定した比率と比べてどうなのかを確認する方法が「2項検定」です。
選択肢を増やせば増やすほど細かい評価が可能になりますが分析も大変になります。
その点、「はい・いいえ」や「有り・無し」などの選択肢が2つしかないケースなら回答する側の負荷も、データを収集・分析する側の負荷も下がります。
2項検定は取り得る値が2つしかない値の分布が「2項分布」に従うことを利用した検定です。
お題「新製品の評価」
#あるソフトウェア開発組織では定期的に製品のバージョンアップを行っている。
製品がリリースされた後に製品の評価をユーザに求めているが、近年では多値での評価ではなく2値(良い・悪い)で評価をしてもらっている。
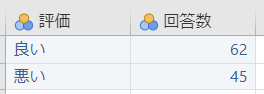
今回のリリースで回収したアンケート総数は全部で107件で、良い・悪いの件数は以下のようだった。
(簡単化のため、未回答のアンケートは無かったとする)
| 良い | 悪い |
|---|---|
| 62 | 45 |
従来では
良い:悪い=7:3
の割合で推移していたが、今回の割合は従来と比較して有意に差があると言えるだろうか。
1標本比例検定「2項検定」
#jamoviを起動し、以下のようにデータを設定します。
注意する点としては、「評価」と「回答数」の両方のデータ型を
データ尺度=「名義尺度」
データ型=「整数」
にすることです。
本来ならば「回答数」データは整数なので連続データのように思いますが、後で度数分布に変換するために、jamoviへの変数登録は「名義尺度」か「順序尺度」を使用する必要があります。今回の場合は「名義尺度」を使用しました。
評価のデータが1,2では分かりづらいので
1:「良い」
2:「悪い」
とラベルを付けます。
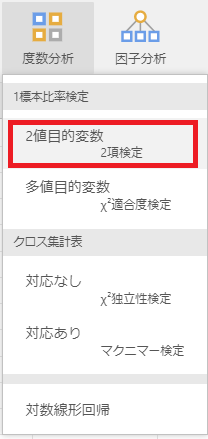
メニューから「分析」-「度数分析」-「2値目的変数(2項検定)」を選択します。
設定パネルが表示されるので、以下のように設定します。
「度数として処理」にチェックを入れると、検定量が設定できるので、ここでは「0.7」(70%)を設定します。
つまり今回の集計結果は
帰無仮説 = 「アンケート結果”良い”=70%」
対立仮説 = 「アンケート結果”良い”≠70%」
と置くことになります。
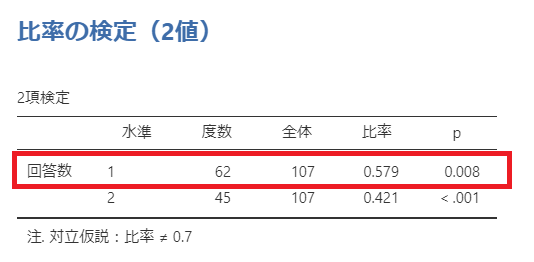
すると以下のような結果が得られました。
水準の1は「良い」の方のデータを指しています。今回利用するのは上段のデータのみです。
p値は「0.008」となっているので「有意差有り」です。
つまり「アンケート結果”良い”=70%」を棄却して、「”良い”=70%とは言えない」ということになります。
ベイズによる検定
#2項検定のオプションを使って「ベイズ統計」で検定してみましょう。
(最近、筆者はベイズ統計にハマっています)
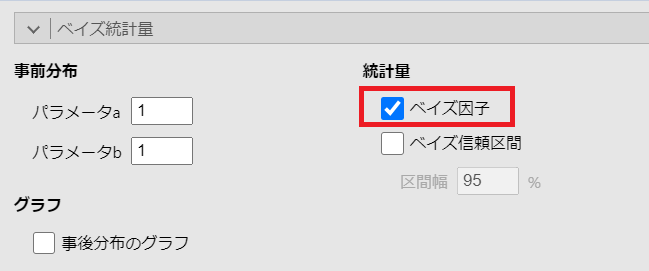
設定で変更する部分は以下の部分です。
パラメータa、パラメータbは「1」のままにしてください。
すると以下のような結果が得られました。
ここでも上段のデータのみ使用します。
ベイズ因子10=3.86
となっています。
ベイズ因子の意味については以前のブログでご説明しましたが、値が3.86程度では「アンケート結果”良い”=70%」を棄却できません。
今回の2項検定でもベイズ統計は古典的統計(推計統計)よりもかなり厳しい判断を下します。
まとめ
#選択肢が2つしか無いときに、選ばれた値の比率が想定した比率と有意に差があるのかを検定することができました。
jamoviでは2項検定において古典的統計(推計統計)とベイズ統計のそれぞれを使って検定することができます。
どちらの検定を使うかは、また2択なんですけどね。悩ましいところです。
データ分析に活用して頂ければ幸いです。