線形回帰を疑ってかかるこれだけの理由
Back to Top今回は「線形回帰」について解説します。
皆さんは「回帰分析」という言葉を一度くらいは聞いたことがあるのではないでしょうか。
線形回帰は統計学で言うところの回帰分析の一つです。
説明変数(入力)を使って従属変数(予測値)を予測します。
線形回帰のうち、説明変数が1つの場合を単回帰、2つ以上の場合を重回帰と呼びます。
今回は線形回帰を使って、説明変数(入力)から従属変数(予測値)を計算する予測式を作ってみましょう。
今回は「仕様書規模(頁)」「レビュー工数(人時)」「レビュー指摘件数(件)」の3つのデータを使って、
- 入力:「仕様書規模(頁)」「レビュー工数(人時)」
- 出力(予測値):「レビュー指摘件数(件)」
の予測式を作ってみたいと思います。
データの確認
#前回ブログ記事と同様にソフトウェア開発部隊から以下のデータを入手しました。(別のプロジェクトから入手したデータなので数値は違っている想定です)
| 仕様書規模(頁) | レビュー工数(人時) | レビュー指摘件数(件) |
|---|---|---|
| 11 | 22 | 5 |
| 13 | 24 | 7 |
| 12 | 23 | 5 |
| 15 | 28 | 8 |
| 11 | 23 | 6 |
| 13 | 25 | 7 |
| 12 | 24 | 6 |
上記のデータをjamoviに入力し「相関行列」を作成して「相関係数」を計算してみましょう。
メニューの「分析」-「回帰分析」-「相関行列」を選択し、以下のように設定します。
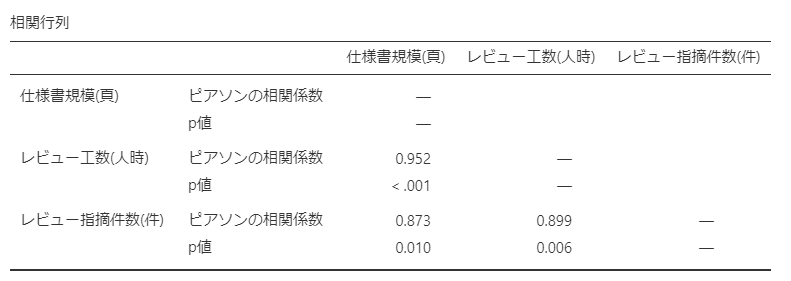
相関行列として以下の表が出力されました。
今回は「仕様書規模(頁)」「レビュー工数(人時)」「レビュー指摘件数(件)」のそれぞれの間に「強い相関(相関係数値 > 0.7)」があることがわかります。
p値も有意を示しています。
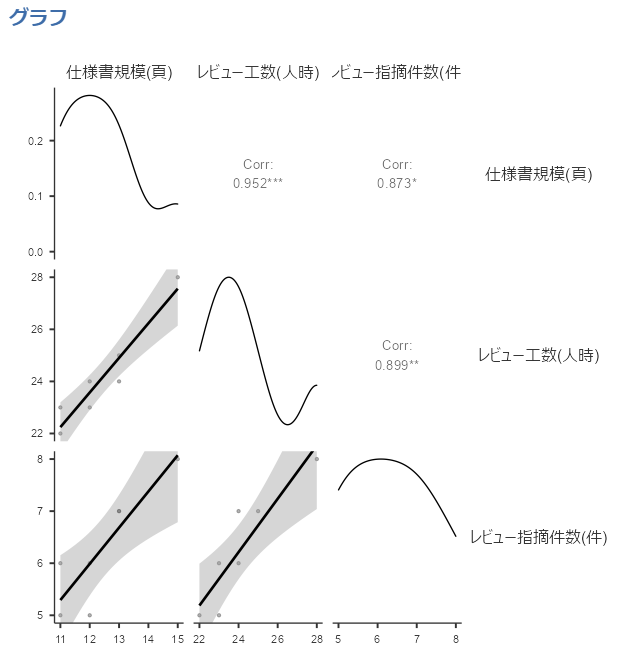
グラフも確認しましょう。
上記グラフからもそれぞれのデータの間に相関があることが見て取れます。
線形回帰
#では、
- 入力:「仕様書規模(頁)」「レビュー工数(人時)」
- 出力(予測値):「レビュー指摘件数(件)」
の予測式を作ってみたいと思います。
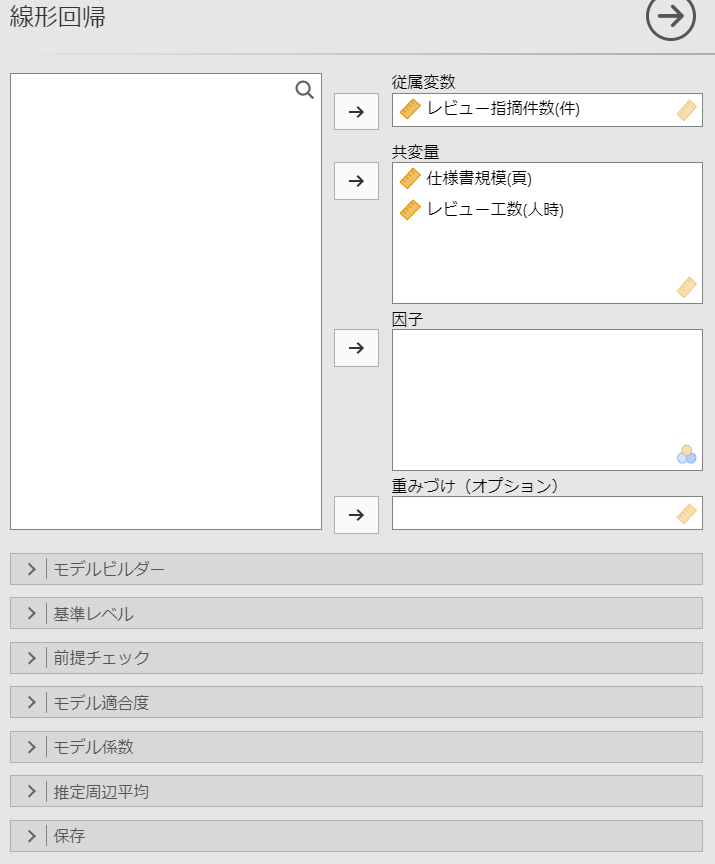
メニューの「分析」-「回帰分析」-「線形回帰」を選択し、以下のように設定します。
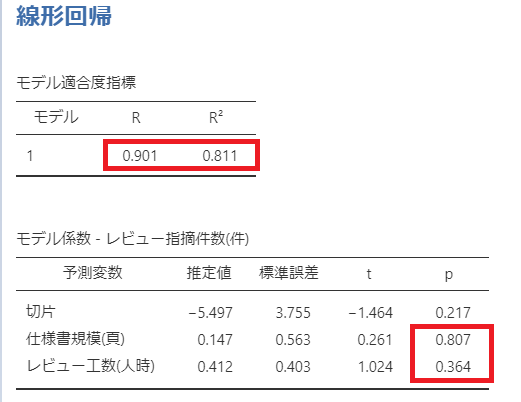
線形回帰として以下の表が出力されました。
モデルの適合度は
R(重相関係数):0.901
R^2(決定係数):0.811
となり、入力(仕様書規模(頁)、レビュー工数(人時))で予測値(レビュー指摘件数(件))が説明できることがわかります。
(モデル係数の中の「切片」は予測式の中の定数項です)
しかし、仕様書規模(頁)、レビュー工数(人時)のモデル係数のp値が有意となっていません。
ここでの検定はモデル係数(回帰係数)が0である可能性があるかどうかをt検定した結果です。
p値から「回帰係数」が0である帰無仮説が棄却できないことがわかります。
モデルの検証
#今回のモデルの取り方に誤りがあったのかもしれません。
そういうときは jamovi の「モデルビルダー」機能を使います。
以下のように設定します。
モデルビルダーでブロック2を追加して
ブロック1:仕様書規模(頁)
ブロック2:レビュー工数(人時)
を指定します。
その結果、分析結果は次のように変わります。
先ほどのブロックの設定により、
モデル1は 説明変数が「仕様書規模(頁)」のみでの回帰結果となり、
モデル2は 説明変数が「仕様書規模(頁)」「レビュー工数(人時)」の2つの時の回帰結果となります。
それぞれを詳しく見ていきます。
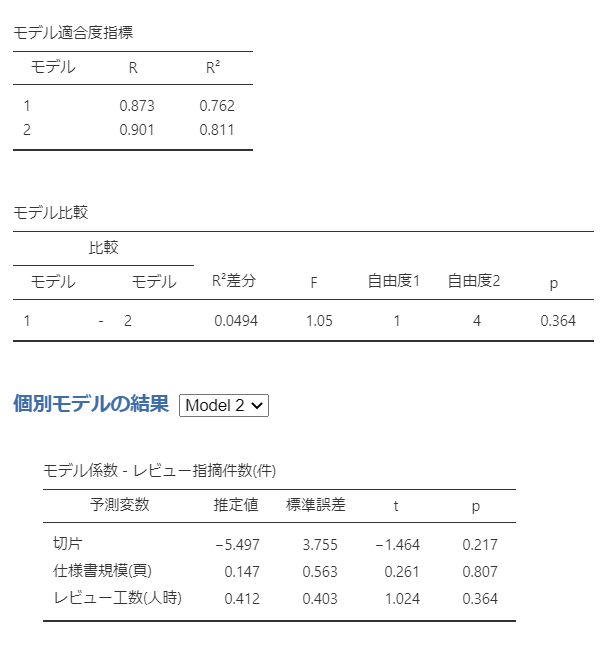
モデル適合度指標を見ると、モデル2の方が値が良いです。
数値だけを見れば、モデル2(説明変数が「仕様書規模(頁)」「レビュー工数(人時)」の2つ)の方が予測が実測に近いと考えられます。
しかし、2つのモデルの間に差はあるのでしょうか?
モデル比較を確認すると、モデル1とモデル2の間に有意な差はないと出ています。(p値が有意基準を満たしていない)
「個別モデルの結果」のプルダウンを使って、モデルを切り替えてみてみましょう。
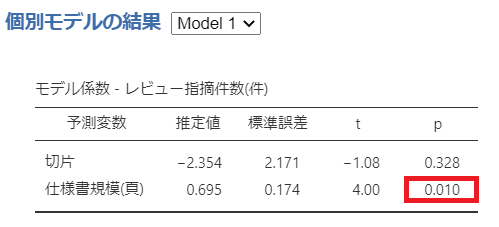
Model1:
Model2:
Model1の場合はp値が有意ですが、Model2の場合はp値が有意になりません。
上記からモデル係数(回帰係数)が有意なのはモデル1ということになります。
前提チェック「共線性統計量」
#線形回帰を実施する上で注意が必要なことがあります。
説明変数の間に強い相関がある場合は、そのまま相関の強い説明変数を含めて分析してしまうと予測式が成り立たなくなる場合があります。
説明変数の相関をチェックするために「多重共線性」を調べます。
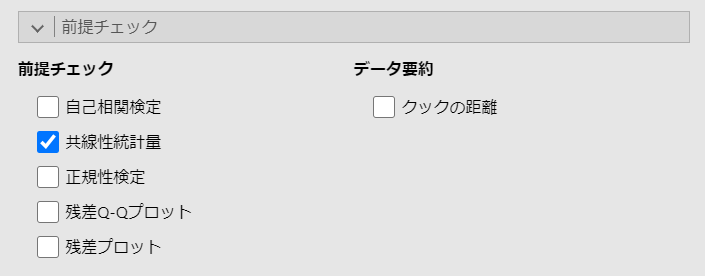
設定項目の事前チェックにある「共線性統計量」にチェックを入れます。
以下のデータが表示されました。
多重共線性が強い場合はVIFの値は1よりも大きくなっていき、5を超えるとかなり多重共線性が強いと言われています。(文献によっては10以上としているものもあります)
今回、5は超えていますので「多重共線性」はあると見ていいでしょう。
これまでの分析から、どうやら説明変数は1つで十分であり、逆に2つの説明変数を使った場合に回帰係数が検定で有意ではない状態になりました。
よって、得られる回帰式は
レビュー指摘件数(件) = 仕様書規模(頁) * 0.695 - 2.354
としました。
(前回のブログでの考察にもあるように、レビュー工数はレビュー会議のやり方によってかなりデータがブレるので、回帰係数には「仕様書規模」を採用しました)
まとめ
#回帰式を作るときに闇雲に説明変数を追加してもダメなことがわかりました。
説明変数を多くすると見た目の相関係数は上昇しますが、回帰式としての価値は下がってしまうこともあるようです。
予測式は非常に魅力的なツールですが、誤った活用をすると出力された結果に右往左往することにもなりかねません。
慎重に利用していく必要があります。
データ分析に活用して頂ければ幸いです。