品質改善効果を検定で確認する
Back to Topデータ分析・解析系の記事をすばやく検索するために Analytics タグを用意しました。
このタグを使って本シリーズ記事を検索していただけたら幸いです。
今回も統計解析ツールjamoviを使ってデータ分析を行っていきます。
お題「品質改善前後の効果の確認」
#今回は品質改善施策を実施する前と実施した後の効果を検定を使って確認していきたいと思います。
お題として以下を考えます。
ある組織で品質改善活動を実施した。
品質改善活動の前後で、ソフトウェアモジュールの結合試験における欠陥密度に変化があったかどうかを確認したい。
改善前と改善後の結合試験結果は以下のサンプルデータを用いて検定する。(結合試験結果はすべて異なるモジュールの試験結果である)
データの単位は欠陥件数/KLocとする。
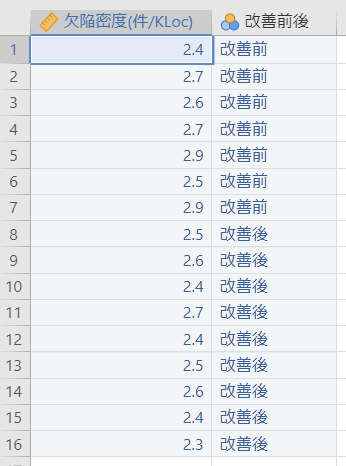
改善前:
2.4
2.7
2.6
2.7
2.9
2.5
2.9
改善後:
2.5
2.6
2.4
2.7
2.4
2.5
2.6
2.4
2.3
さっそくjamoviにデータを設定します。
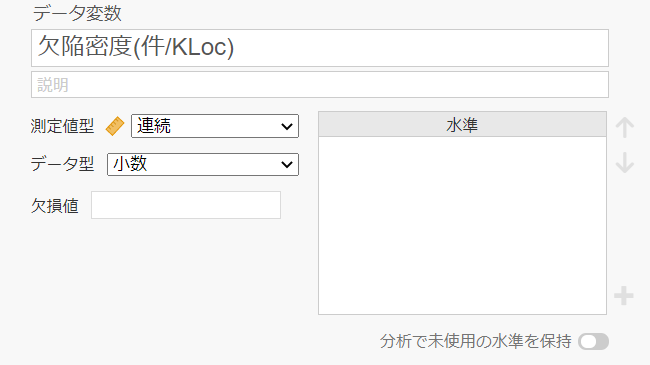
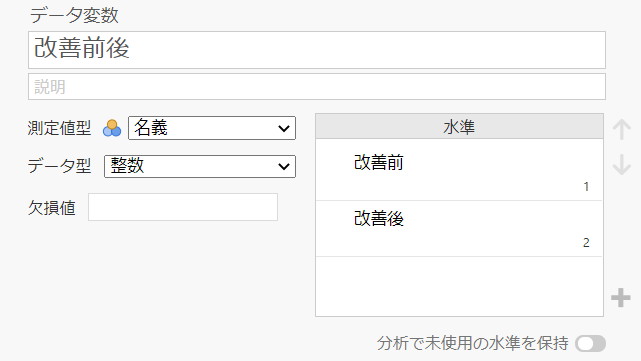
今回は欠陥密度データ以外に、データが改善前なのか後なのかが区別できるような名義変数を追加しています。
改善前後を表す変数として「改善前後」という名義変数を設定しています。後に検定で使用します。
変数A列:欠陥密度(件/KLoc)
変数B列:改善前後
データパネル
記述統計での確認
#メニューの「分析」-「探索」-「記述統計」を選択します。
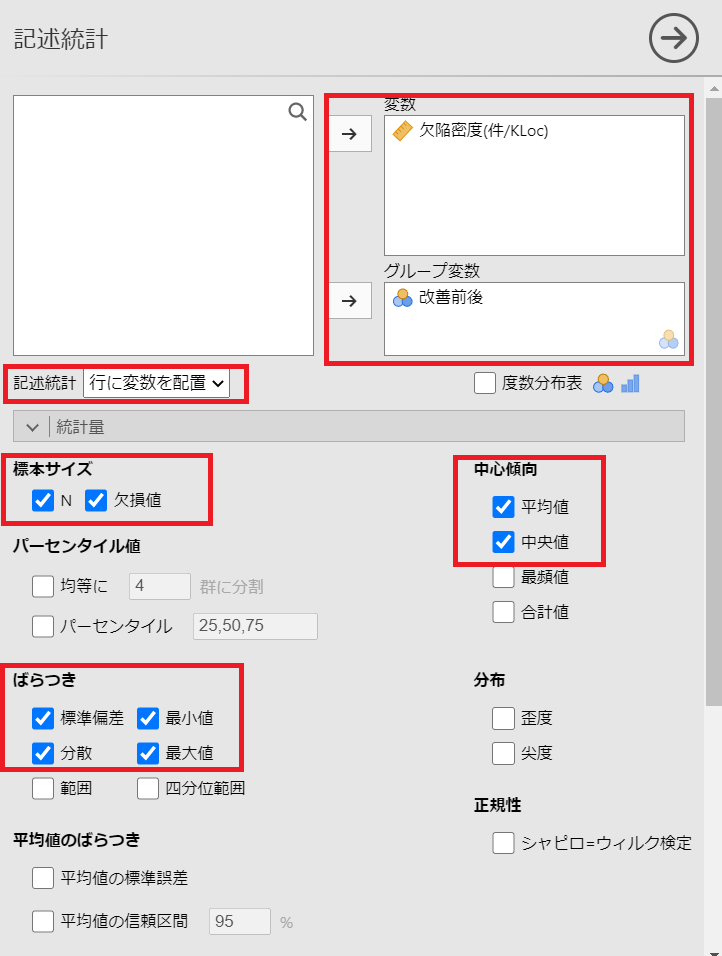
統計量の設定を以下のように行います。
(記述統計「行に変数を配置」を選択しています)
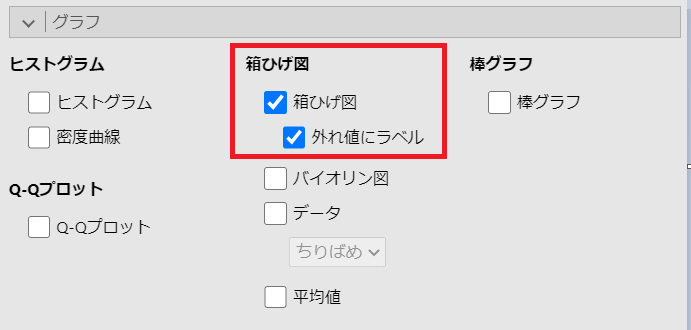
グラフの設定は「箱ひげ図」を設定します。
記述統計データが以下のように表示されました。
平均値と中央値の値は、改善前よりも改善後の方が小さくなっています。
感覚的にですが、改善効果として「欠陥密度が下がった」ように見えます。
現段階ではまだ推測の域を出ていません。
次にグラフでも確認しましょう。
箱ひげ図での確認
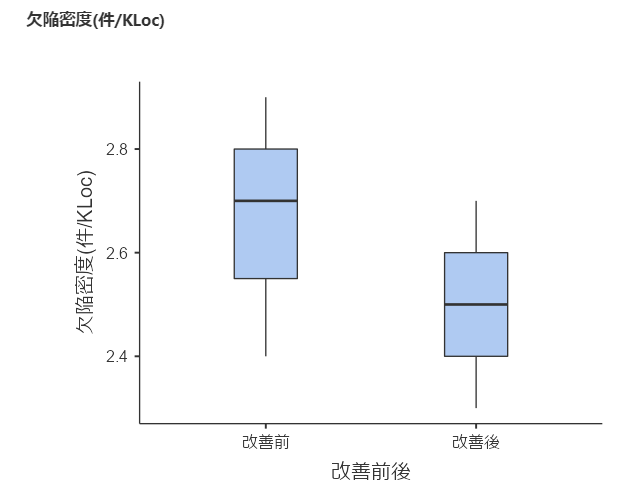
#箱ひげ図は以下のように表示されました。
これも”視覚的”には、改善前よりも改善後の欠陥密度が全体的に下がっているように見えます。
これらを踏まえて、改善効果があったことを”定量的”に確認していきます。
t検定の種類
#今回もまた「t検定」の登場です。
これまでのブログ記事でもt検定を用いてきました。
jamoviが提供しているt検定機能には
・対応のないt検定
・対応のあるt検定
・1標本t検定
の3つがあります。
1標本t検定をどのように使うかについては、これまでの記事
・統計解析ツールjamoviの紹介
・箱ひげ図で外れ値を確認する
を参照ください。
t検定とは「t分布」を使った仮説検定です。
t分布についてはここでは深く言及しませんが、連続確率分布の1つで、平均の推定によく用いられます。
仮説検定について話すと長くなるのですが、簡単にいうと「ある仮説を設定して、その仮説の正否を確率で判断する手法」と言えます。
私の解釈では仮説検定は少しひねくれた物の考え方のように思いますが、そうしないと説明できない場合もあるのでしょう。
「対応なしt検定」と「対応ありt検定」について簡単に説明します。
- 対応なしt検定とは
互いに独立した2つのグループの間で母集団の平均値の差の有無を検定する手法です。
独立した2つのグループのデータ数は一致していなくてもいいです。(独立なので)
今回の例題のように、改善前と改善後などの別々の「関連なく独立した」データに対しての検定に使えます。
- 対応ありt検定とは
上記の「対応なしt検定」とは違い、対応がある2群の差が0かどうかについての検定手法です。
例えば、旧来の薬と新薬を”同じ”被験者が試したときのデータなどは、同一人物が2つの異なるアクションをとっているので、これらのデータ群を検定するときには「対応ありt検定」を用います。
この場合、データは独立して”いない”ので、検定対象のそれぞれのデータ数は同じになります。
講釈はこの辺にして、作業を先に進めましょう。
今回の例題では「対応なしt検定」を選択します。
対応なしt検定での確認
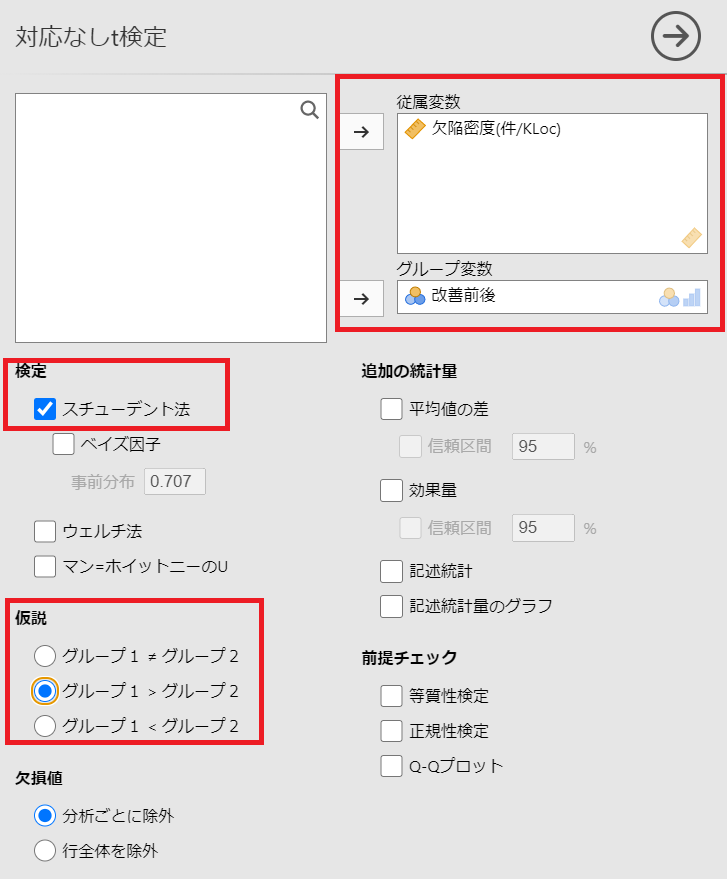
#メニューの「分析」-「t検定」-「対応なしt検定」を選択し、以下のように設定します。
対立仮説として「改善前よりも改善後の方が値が小さいこと」にしたいので、仮説の部分は
グループ1 > グループ2
としています。
(名義変数で、改善前:グループ1、改善後:グループ2 と設定しています)
検定結果として以下の値が得られました。
p値は0.018で5%以下なので、帰無仮説(改善前と改善後は同じ)は棄却され、
欠陥密度は「改善前 > 改善後」と言える、となりました。
まとめ
#平均値、中央値、箱ひげ図で確認した”見た目”の差が定量的に検定で確認できました。
今回の例題のように、何かの施策後の効果を確認したいケースは他にもたくさんあると思います。
注意したいことは、今回の結果はあくまで”試験の結果”の差であって、そうなった原因の特定はしていないことです。テストでの欠陥除去率が低くなっただけ(つまり改悪)かもしれません。
一つの検定だけで満足せずに、他のいろいろな側面から効果の確認をしていく必要があります。
少しでも統計に興味を持っていただければ幸いです。