箱ひげ図で外れ値を確認する
Back to Top前回のブログ記事では統計解析ツールjamoviを使って1標本t検定を行う例をご紹介しました。
今回は再度jamoviを使いつつ、データ分析をする上でネックになる”外れ値”を箱ひげ図を使って確認し、分析に適用していく方法をご紹介します。
外れ値とは
#データ分析を実施していると、値自体は「異常」ではないが「他の値から大きく外れた値」が分析をする上で問題になることがあります。この「他の値から大きく外れた値」のことを統計では「外れ値」と呼んでいます。
正常な活動の結果でありながら、他のデータにとって外乱となり、統計分析を実施していく上で不都合を生じさせることがあります。
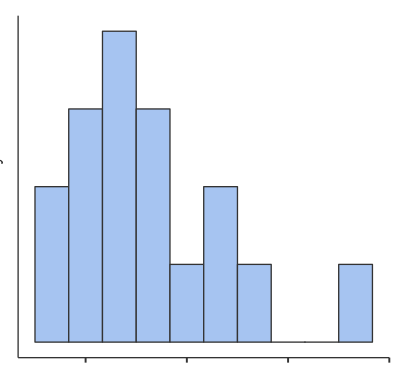
分析対象のデータ群からヒストグラムを作成して、外れ値を”目視”で確認する方法で外れ値を見つけることはできます。(母集団が正規分布に従うと仮定)
上記の例では一番右側のデータが外れ値ではないかと推測できます。
これはあくまで人間が”目視”で確認しているので、もう少しシステマチックに外れ値を確認したいと思います。
箱ひげ図とは
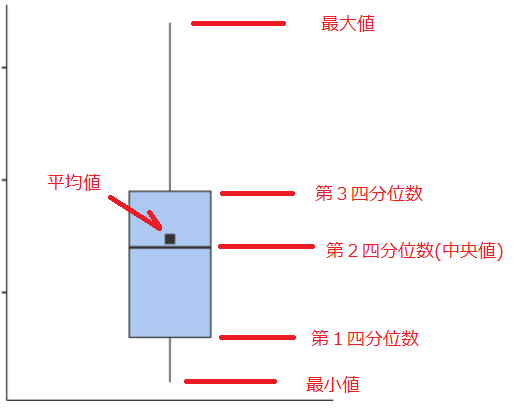
#箱ひげ図とは、下図に示すように最小値、第1四分位数、第2四分位数(中央値)、第3四分位数、最大値を持ち、第1四分位数から第3四分位数までの範囲を箱で描画し、最小値、最大値は箱の両端からそれぞれ線を引き出した図です。
箱は第2四分位数(中央値)で区切ってあります。
(今回はオプションで平均値を箱の中に黒点で示しています)
箱ひげ図の特徴は
- 最小値から中央値までの間に全データのうちの下側50%のデータが入る
- 中央値から最大値までの間に全データのうちの上側50%のデータが入る
- 箱の中に中央値を中心にして全データのうちの上下50%のデータが入る
です。
箱の形とひげ(線)の長さを見れば、データがどのように散らばっているかについて、おおよその見当がつきます。
もし最小値や最大値が”もの凄く”他の値から離れていた場合は、箱ひげ図の描画はどうなってしまうのでしょうか?
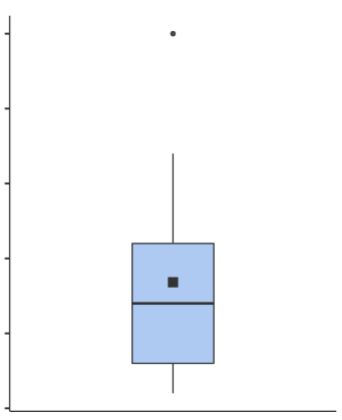
箱ひげ図によく用いられるルールとして、第1四分位数から第3四分位数の距離(つまり箱の長さ)の1.5倍以上箱から離れた値は”外れ値”として別途描画し、外れ値を除外したデータで箱ひげ図を描画します。
上記の図では外れ値(上側外れ値)が1点あります。
全体的に、箱の形も間延びせずまとまりがあるように見えます。
このように、箱ひげ図ではルールとして外れ値を除外して描画する仕組みがあります。
箱ひげ図を使って外れ値を確認していく
#箱ひげ図を手作業で描画するのは意外と面倒ですが、最近は便利なツールがありますので利用していきましょう。
前回同様に「ソフトウェアモジュール群」の「欠陥密度」の1標本t検定の例で説明します。
jamoviの箱ひげ図で”外れ値”を確認しつつ分析を行います。
また、データにフィルタを適用して外れ値を除外する方法をご紹介します。
例題
開発した多数のソフトウェアモジュール群の結合試験を実施している。
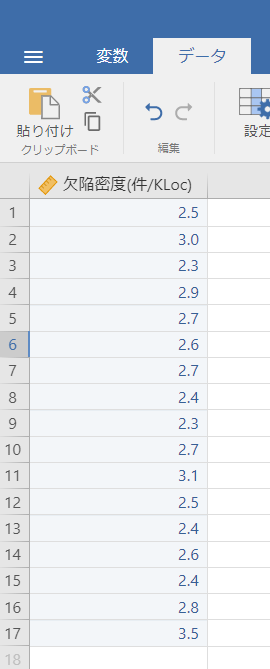
すでに結合試験が完了しているソフトウェアモジュール(17個)の欠陥密度は以下のようであった。
部門で決めている合否基準が「2.5」とした場合、現段階でモジュール群の欠陥密度は合否基準と照らし合わせて明確に”差”があると言えるか?
欠陥密度(件/KLoc)
2.5
3.0
2.3
2.9
2.7
2.6
2.7
2.4
2.3
2.7
3.1
2.5
2.4
2.6
2.4
2.8
3.5
準備としてjamoviに上記のデータを設定します。
外れ値を除外しない検定
#外れ値をデータから除外せずに、そのまま箱ひげ図を描画させます。
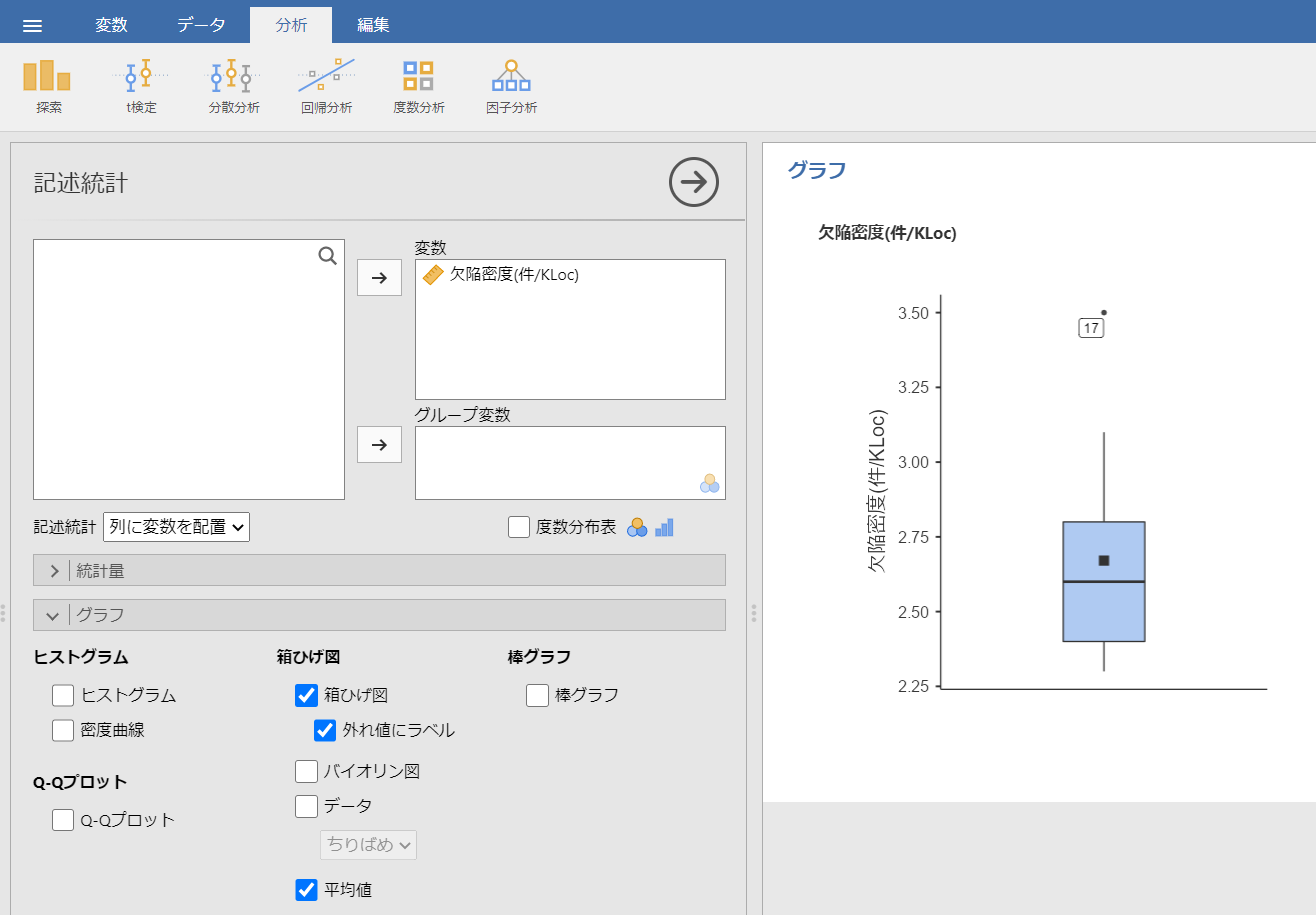
メニューの「分析」-「探索」-「記述統計」を選択し、以下のように設定します。
箱ひげ図をチェックオンして、「外れ値にラベル」もチェックします。
図からNo.17のデータ(値:3.5)が外れ値であることがわかります。
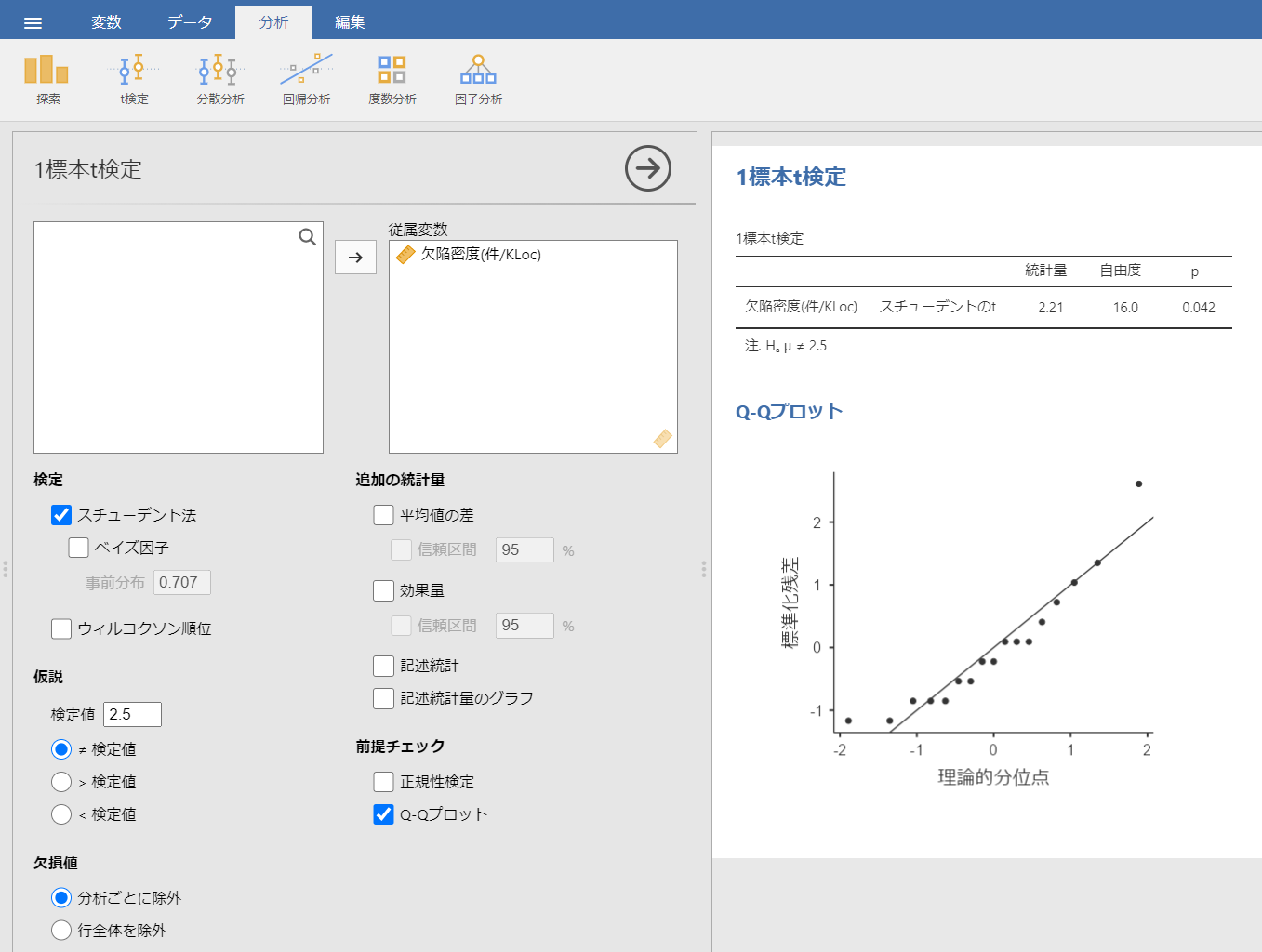
次に、メニューの「分析」-「t検定」-「1標本t検定」を選択し、以下のように設定します。
ついでに「Q-Qプロット」もチェックオンします。
検定結果のp値は0.042となり5%未満なので、帰無仮説は棄却され「基準(2.5)と差がある」という結果になりました。
しかし、Q-Qプロットで図で見ると、やはり外れ値の存在が気になります。
(Q-Qプロットはデータの分布が正規分布になっているかどうかを視覚的に確認できます)
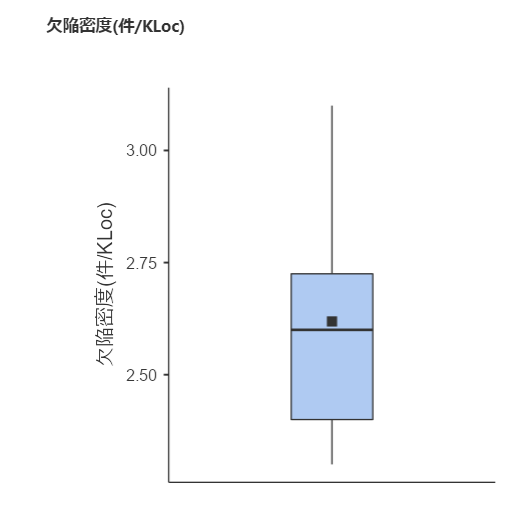
外れ値を除外して検定
#先ほどの箱ひげ図で見たNo.17(値:3.5)をデータから除外して検定をやり直してみましょう。
除外といってもデータパネルからデータを”本当に”削除してしまわずに、データフィルタを使って一時的にデータを”無いもの”として扱います。
(フィルタはON/OFFできます)
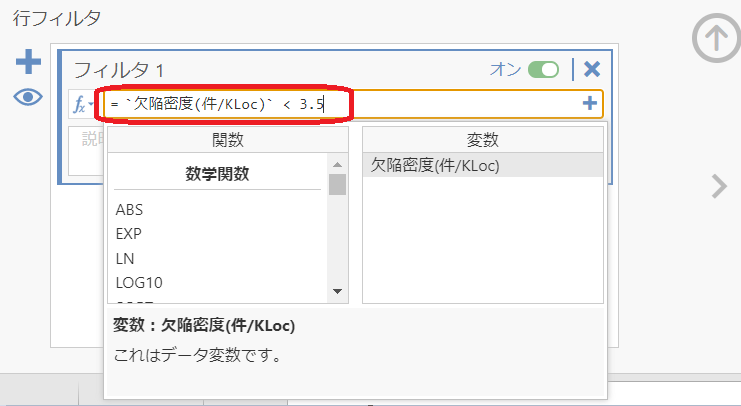
メニューの「データ」-「フィルタ」を選択します。
行フィルタという設定パネルが表示されます。
フィルタ1として、
= `欠陥密度(件/KLoc)` < 3.5
を設定します。
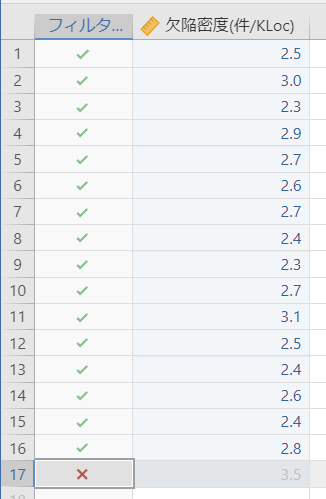
するとデータパネル上で、フィルタされたデータが半輝度になって無効化されているのがわかります。
すぐに箱ひげ図にもデータが反映され、箱ひげ図上から外れ値が消えていることがわかります。
図で見る限り”外れ値”は描画されていません。
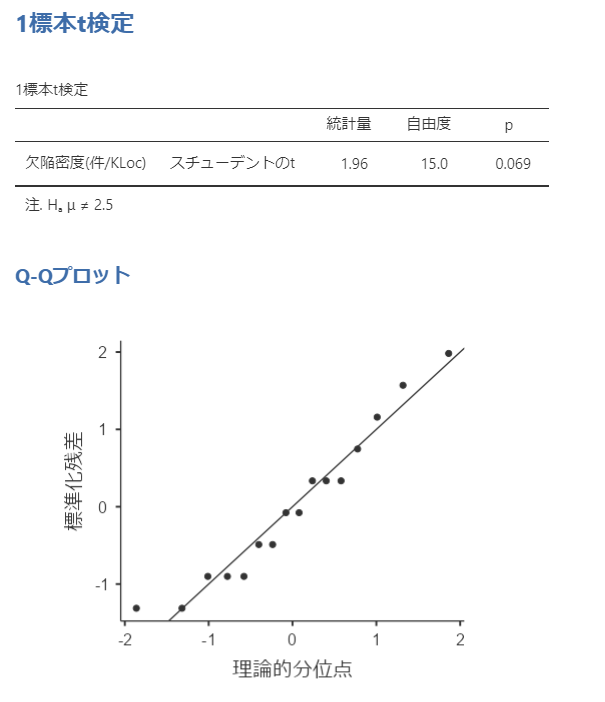
再度、1標本t検定を実施してみましょう。
今度はp値が0.069となり5%以上になっています。帰無仮説は棄却できず「基準(2.5)との差はない」という結果になりました。
今回のQ-Qプロット図を確認しても、外れ値込みだったQ-Qプロット図よりは正規分布に近そうです。
(本当は厳密に判断すべきなんでしょうが、今回は箱ひげ図による外れ値チェックの例なので、この程度にとどめます)
今回の例では、外れ値を含む場合と含まない場合で検定結果に違いが出ました。
まとめ
#外れ値が検定に与える影響について見てきました。
人間が視覚的に外れ値を「なんとなく」除外するのではなく、決まったルールで外れ値を除外することによって、部門・プロジェクト・チーム毎に違った分析結果になることなく情報を共有できるようになると期待できます。
また、外れ値を確認することで、そのデータが「どうしてそうなった?」について検討する機会も得ることができます。
活動の特異点を早めに発見して、対処することも可能になると思います。
ぜひ「箱ひげ図」をご活用ください。